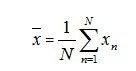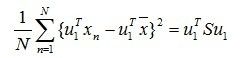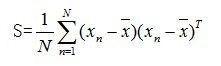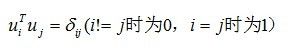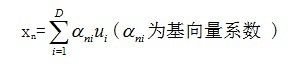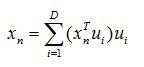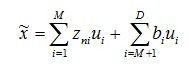PCA
PCA（Principal Component Analysis),称主成分分析，从统计学的角度来说是一种多元统计方法。PCA通过将多个变量通过线性变换以选出较少的重要变量。它往往可以有效地从过于“丰富”的数据信息中获取最重要的元素和结构，去除数据的噪音和冗余，将原来复杂的数据降维，揭示隐藏在复杂数据背后的简单结构。近年来，PCA方法被广泛地运用于计算机领域，如数据降维、图像有损压缩、特征追踪等等。
在人脑的生理特征中，人脑对外界的认知手段多样，导致人获取的信息维数过高。如果人脑不对获取的信息进行降维处理，那么人脑对信息处理的效率和精准度都会下降，因此人脑对这些感知神经处理时，均通过了复杂的降维处理。
PCA方法广泛运用于从神经科学到计算机图形学的数据分析。因为它是一种简单的非参方法，能够从复杂的数据集中提取出数据相关信息。我们进行主成分分析的动机是希望计算出一个含有噪音数据空间的最重要的基，来重新表达这个数据空间。但是这些新基往往隐藏在复杂的数据结构中，我们需要滤除噪音来找到重构出数据空间的新基。
PCA方法是一个高普适用方法，它的一大优点是能够对数据进行降维处理，我们通过PCA方法求出数据集的主元，选取最重要的部分，将其余的维数省去，从而达到降维和简化模型的目的，间接地对数据进行了压缩处理，同时很大程度上保留了原数据的信息，就如同人脑在感知神经处理时进行了降维处理。
所以在机器学习和模式识别及计算机视觉领域，PCA方法被广泛的运用。
在人脸识别中，假设训练集是30幅不同的N×N大小的人脸图像。把图像中每一个像素看成是一维信息，那么一副图像就是N2维的向量。因为人脸的结构有极大的相似性，如果是同一个人脸的话相似性更大。而我们的所希望能够通过人脸来表达人脸，而非用像素来表达人脸。那么我们就可以用PCA方法对30幅训练集图像进行处理，寻找这些图像中的相似维度。我们提取出最重要的主成份后，让被识别图像与原图进行过变化后的主元维度进行相似度比较，以衡量两幅图片的相似性。
在图像压缩方面，我们还可以通过PCA方法进行图像压缩，又称Hotelling或者Karhunen and Leove变换。我们通过PCA提取出图像的主分量，去除掉一些次分量，然后变换回原图像空间，图像因为维数的降低得到了很大程度上的压缩，同时图像还很大程度上保留了原图像的重要信息。
正文：
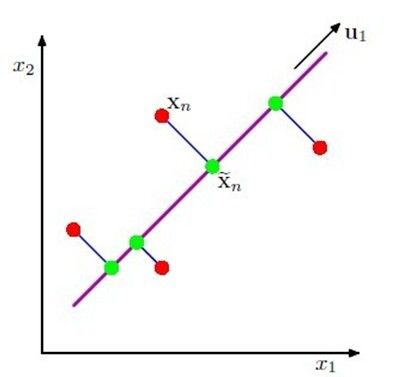
PCA方法其实就是将数据空间通过正交变换映射到低维子空间的过程。而相应的基向量组应满足正交性且由基向量组构成的地位子空间最优地考虑了数据的相关性。在原数据集变换空间后应使单一数据样本的相互相关性降低到最低点。
图1 红点代表原始数据点；绿点代表被映射到低维空间后的点；紫线代表映射平面。
方差最大化上面我们说过PCA方法的过程其实是寻找低维子空间的过程。那么什么样的低维空间才符合我们要求的呢。因为我们希望被映射后的数据之间的相关性降低到最低点，所以我们可以采取求解被映射后方差最大化的最优策略来找到低维空间。
假设我们有N个样本数据{xn},每个样本数据是D维，我们希望样本数据映射到M<D维的子空间，并且使映射后的数据方差最大化。为了使问题简单化，我们令M=1,即映射到1维空间。我们设低维空间的方向向量为D维单位向量u1,并且具有正交性,即u1Tu1=1。那么每一个样本数据点xn被映射到1维空间后就表示成了u1Txn。我们令原始N个样本数据均值向量为
（1）
那么映射后的数据方差就为：
（2）
注：此处S为原始数据集的协方差矩阵
（3）
我们所希望的低维空间是能使等式（2）值最大的空间，即方差最大化。那么问题就转化为求解等式（2）的最大值。
因为u1向量是正交向量，所以我们引入拉格朗日乘子法求解等式（2）得最大值。构造条件限制等式：
（4）
由高等数学知识可知，我们要求解关于u1的等式（4）的最大值，只需要令（4）对u1求导令其等于0，得：
（5）
由线形代数知识可知，
必为协方差矩阵的特征值，而u1为其对应的特征向量。
我们将由1维情况扩展到M>1维情况，协方差矩阵S应该有M个特征特征值：
，其对应的特征向量应为：u1,…,un。
PCA的另一种构造形式是基于误差最小化。
我们引入D维完备正交基向量组，即
（6）
所以我们可以用完备正交基向量来线形表示样本数据集中的每一个数据xn，
（7）
充分利用根据等式（6）的正交属性，利用等式（7）可得系数 
,反代回等式（7），可得等式：
（8）
我们来看，表达等式（8）需要D维信息，而我们的目的是希望用M<D维信息近似地表达出xn：
（9）
代表的是数据点的特殊分量，而bi代表的是所有数据点的所共有的分量。我们构造一个目标函数:
（10）
其通俗的含义是我们希望通过M维表达的出的数据点逼近D维样本数据点,这里我们采用欧式距离衡量两个数据点的相似性。那么我们的问题又转化为最小化目标函数J。通过求导，我们可以得出：
（11）
（12）
反代回等式（10），得：
（13）
因此我们只要找寻协方差矩阵S的D-M个最小特征值就可。
SVD奇异值分解PCA方法中对于协方差矩阵的分解，提取主成分，采用两种方法：
1 特征值分解。该种方法有一定局限性，分解的矩阵必须为方阵。
2 SVD奇异值分解。
奇异值分解是线性代数中的一种重要的矩阵分解方法，在信号处理、统计学等领域都有重要的应用。奇异值分解可以将一个比较复杂的矩阵分解为几个更小更简单的子矩阵相乘的形式来表达，而这些子矩阵描述的是原矩阵的重要的特性。
对于一个M×N大小的矩阵A来说，总是可以分解为:
（14）
其中U和V分别是AAT和ATA的特征向量，而
则是他们的特征根。在PCA方法中，我们选取P个最大特征根及其所对应的特征向量，对A进行逼近：
（15）