迪杰斯特拉算法处理有向图中最短路径的(dijkstra)Java实现及升级
程序中要用到最短路径的寻找,就用了迪杰斯特拉算法,在网上找了个实现,然后自己又升了下级,如下:
package reverse;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.PriorityQueue;
public class DijSuccess {
public static int INFINITY = 99999;
public static Map<String,Vertex> vertexMap = new HashMap<String,Vertex>();
//边距
static class Edge{
public Vertex dest;
public double cost;
public Edge(Vertex d,double c){
this.dest = d;
this.cost = c;
}
}
//静态类:Vertex
static class Vertex implements Comparable<Vertex>{
public String name;
public List<Edge> adj;
public double dist;
public Vertex prev;
public int scratch;
public boolean visited;
public Vertex(String nm){
this.name = nm;
adj = new ArrayList<Edge>();
reset();
}
public void reset(){
visited = false;
dist=DijSuccess.INFINITY;
}
@Override
public int compareTo(Vertex o) {
double c = o.dist;
return dist < c ? -1:dist > c ? 1:0;
}
}
//dijkstra算法实现:找到从startName点出发,到其他所有点的最短路径:选取自己定义的终点
public static void dijkstra(String startName,String endName){
PriorityQueue<Vertex> pq = new PriorityQueue<Vertex>();//该队列以权值升序排列,因为Vertex实现Comparable接口
Vertex start = vertexMap.get(startName);
start.dist = 0;
for(Vertex v:vertexMap.values())
pq.add(v);
int seenNum = 0;
while(!pq.isEmpty()&&seenNum < vertexMap.size()){
Vertex v = pq.remove();
if(v.name.equals(endName)){ //恰好是自己要找的那个点
System.out.println(startName + "---->" + v.name + ":" + v.dist);
System.out.println(getPreNames(v));
break;
}
if(v.scratch != 0)
continue;
v.scratch = 1;
seenNum++;
for(Edge e:v.adj){
Vertex w = e.dest;
double v_to_w = e.cost;
if(w.dist > v.dist + v_to_w){
w.dist = v.dist + v_to_w;
w.prev = v;
pq.remove(w);//出队
pq.add(w);//按优先级插在队头,先插入的在队头,依次往后
}
}
}
System.out.println("hello!");
while(pq.peek() != null ){
System.out.println(pq.poll());
}
}
/**
* 得到最短路径所经历的路线
* seven
* @param v
* @return
*/
public static String getPreNames(Vertex v){
String routeEndName = v.name;
StringBuilder sb = new StringBuilder();
while(v.prev != null){
sb.append(v.prev.name + ",");
v = v.prev;
}
String reverseRoute = routeEndName + "," + sb.toString();
String[] reverseArray = reverseRoute.split(",");
StringBuilder route = new StringBuilder();
for(int i=0;i<reverseArray.length;i++){
route.append(reverseArray[reverseArray.length-1-i]);
route.append(",");
}
return route.substring(0, route.length()-1);
}
public static void main(String[] args){
Vertex v1 = new Vertex("v1");
Vertex v2 = new Vertex("v2");
Vertex v3 = new Vertex("v3");
Vertex v4 = new Vertex("v4");
Vertex v5 = new Vertex("v5");
List<Edge> e1l = v1.adj;
List<Edge> e2l = v2.adj;
List<Edge> e3l = v3.adj;
List<Edge> e4l = v4.adj;
List<Edge> e5l = v5.adj;
Edge e12 = new Edge(v2,10);
Edge e14 = new Edge(v4,30);
Edge e15 = new Edge(v5,100);
e1l.add(e14);
e1l.add(e15);
e1l.add(e12);
Edge e23 = new Edge(v3,50);
e2l.add(e23);
Edge e35 = new Edge(v5,10);
e3l.add(e35);
Edge e43 = new Edge(v3,20);
Edge e45 = new Edge(v5,60);
e4l.add(e43);
e4l.add(e45);
/*
以上代码构建有向图
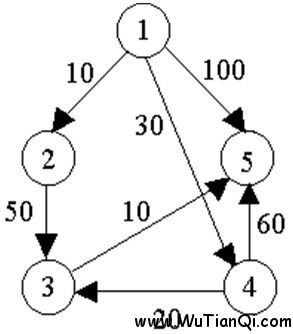
v1---->v5:100
v1----->V4:30
v1------>V2:10
V2------>V3:50
V3------->V5:10
v4------->V3:20
v4------->V5:60
*/
vertexMap.put("v1", v1);
vertexMap.put("v2", v2);
vertexMap.put("v3", v3);
vertexMap.put("v4", v4);
vertexMap.put("v5", v5);
dijkstra("v1","v5");
}
}
算法 的大致说明:
用PriorityQueue来做数据存储。
开始记录了所有的点,及默认的距离。
然后拿出一个点A,再计算其余的点通过点A来到达的距离,选择其中最短的,得到点B。再选择通过点B............最终达到目的。
在网上看到实现不是指定终点的,而是指点起点,便将到其他点的最短路径都罗列出来。
//dijkstra算法实现
public static void dijkstra(String startName){
PriorityQueue<Vertex> pq = new PriorityQueue<Vertex>();//该队列以权值升序排列,因为Vertex实现Comparable接口
Vertex start = vertexMap.get(startName);
start.dist = 0;
for(Vertex v:vertexMap.values())
pq.add(v);
int seenNum = 0;
while(!pq.isEmpty()&&seenNum < vertexMap.size()){
Vertex v = pq.remove();
System.out.println("v0---->"+v.name+":"+v.dist);
if(v.scratch != 0)
continue;
v.scratch = 1;
seenNum++;
for(Edge e:v.adj){
Vertex w = e.dest;
double v_to_w = e.cost;
if(w.dist > v.dist + v_to_w){
w.dist = v.dist + v_to_w;
w.prev = v;
pq.remove(w);//出队
pq.add(w);//按优先级插在队头,先插入的在队头,依次往后
}
}
}
System.out.println("hello !");
while(pq.peek() != null ){
System.out.println(pq.poll());
}
}