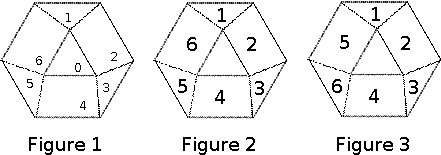
poj 3221Diamond Puzzle(bfs+状压)
| Time Limit: 2000MS | Memory Limit: 131072K | |
| Total Submissions: 1394 | Accepted: 762 |
Description
A diamond puzzle is played on a tessellated hexagon like the one shown in Figure 1 below. And in this problem the faces produced by the tessellation are identified as they are numbered in the same figure. If two faces share a side, they are called neighboring faces. Thus, even-numbered faces have three neighboring faces, while odd-numbered faces have only two. At any point during the play of the puzzle, six of the seven faces hold a unique digit ranging from 1 to 6, and the other one is empty. A move in the puzzle is to move a digit from one face to a neighboring empty one.
Starting from any configuration, some series of moves can always make the puzzle look identical to either one shown in Figures 2 and 3. Your task is to calculate the minimum number of moves to make it become the one inFigure 2.
Input
The input contains multiple test cases. The first contains an integer N (0 ≤ N ≤ 5,040), the number of test cases. Then follow N lines, each with a permutation of {0, 1, 2, 3, 4, 5, 6} describing a starting configuration of the puzzle. The ith digit in the permutation is the one in the face numbered i − 1. A zero means the face is empty.
Output
For each test cases, output the minimum number of moves the configuration takes to reach the one shown in Figure 2. If this is impossible, just output “-1” and nothing else.
Sample Input
3 1324506 2410653 0123456
Sample Output
10 -1 0
Source, wenxichang
题意:图中7个位置,有6个数字,与空位置有相邻边的数字可跳进空位置,求最少步数从给定状态到达目标状态。所给数据第i个即为Figure1中标号i-1格子的数字,Figure2为目标状态。
思路:状态压缩存状态,状态大约5040,做好映射就行。注意 N (0 ≤ N ≤ 5,040),所以不能从所给状态往终点搜,正确做法是从终点bfs向其他点搜索全图,将步数存下,随用随取,否则应该就超时了。
代码:
#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
int done[1<<21];
int sx,ex;
struct node
{
int x,w,cc;
node(int xx=0,int ww=0,int ccc=0)
{
x=xx;w=ww;cc=ccc;
}
}que[10000];
int forin[7][3]={6,2,4,2,6,0,0,1,3,2,4,0,0,3,5,4,6,0,0,1,5};
void bfs()
{
int i,db[9],st=0,en=0;
memset(done,-1,sizeof done);
done[ex]=0;
que[en++]=node(ex,0,0);//最后的0为空位置的初始位置
while(st<en)
{
node e=que[st++];
int ccc=e.cc;
int tt=2+!(ccc%2);
for(i=0;i<tt;i++)
{
int yy=((e.x)>>(forin[ccc][i]*3))%8;
int cur=e.x^(yy<<(forin[ccc][i]*3))|(yy<<(ccc*3));//^可清除目标位置forin[ccc][i]数字,|将yy放在ccc位
if(done[cur]!=-1)continue;
que[en++]=node(cur,e.w+1,forin[ccc][i]);
done[cur]=e.w+1;
}
}
}
int main()
{
int N,n,m,i;char da[100];
ex=1754760;
bfs(0);
scanf("%d",&N);gets(da);
while(N--)
{
gets(da);
for(sx=0,i=0;i<7;i++)
{
sx|=((da[i]-'0')<<(i*3));
}
printf("%d\n",done[sx]);
}
return 0;
}