I assume entropy was mentioned in the context of building decision trees.
To illustrate, imagine the task of learning to classify first-names into male/female groups. That is given a list of names each labeled with either m or f, we want to learn a model that fits the data and can be used to predict the gender of a new unseen first-name.
name gender
----------------- Now we want to predict
Ashley f the gender of "Amro" (my name)
Brian m
Caroline f
David m
First step is deciding what features of the data are relevant to the target class we want to predict. Some example features include: first/last letter, length, number of vowels, does it end with a vowel, etc.. So after feature extraction, our data looks like:
# name ends-vowel num-vowels length gender
# ------------------------------------------------
Ashley 1 3 6 f
Brian 0 2 5 m
Caroline 1 4 8 f
David 0 2 5 m
The goal is to build a decision tree. An example of a tree would be:
length<7
| num-vowels<3: male
| num-vowels>=3
| | ends-vowel=1: female
| | ends-vowel=0: male
length>=7
| length=5: male
basically each node represent a test performed on a single attribute, and we go left or right depending on the result of the test. We keep traversing the tree until we reach a leaf node which contains the class prediction (m or f)
So if we run the name Amro down this tree, we start by testing "is the legth<7?" and the answer is yes, so we go down that branch. Following the branch, the next test "is the number of vowels<3?" again evaluates to true. This leads to a leaf node labeled m, and thus the prediction is male (which I happen to be, so the tree predicted the outcome correctly).
The decision tree is built in a top-down fashion, but the question is how do you choose which attribute to split at each node? The answer is find the feature that best splits the target class into the purest possible children nodes (ie: nodes that don't contain a mix of both male and female, rather pure nodes with only one class).
This measure of purity is called the information. It represents the expected amount ofinformation that would be needed to specify whether a new instance (first-name) should be classified male or female, given the example that reached the node. We calculate it based on the number of male and female classes at the node.
Entropy on the other hand is a measure of impurity (the opposite). It is defined for a binary class with values a/b as:
Entropy = - p(a)*log(p(a)) - p(b)*log(p(b))
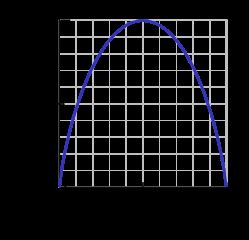
This binary entropy function is depicted in the figure below (random variable can take one of two values). It reaches its maximum when the probability is p=1/2, meaning that p(X=a)=0.5 or similarlyp(X=b)=0.5 having a 50%/50% chance of being either a or b(uncertainty is at a maximum). The entropy function is at zero minimum when probability is p=1 or p=0 with complete certainty (p(X=a)=1 or p(X=a)=0 respectively, latter implies p(X=b)=1).
Of course the definition of entropy can be generalized for a discrete random variable X with N outcomes (not just two):
(the log in the formula is usually taken as the logarithm to the base 2)
Back to our task of name classification, lets look at an example. Imagine at some point during the process of constructing the tree, we were considering the following split:
ends-vowel
[9m,5f] <--- the [..,..] notation represents the class
/ \ distribution of instances that reached a node
=1 =0
------- -------
[3m,4f] [6m,1f]
As you can see, before the split we had 9 males and 5 females, i.e. P(m)=9/14 and P(f)=5/14. According to the definition of entropy:
Entropy_before = - (5/14)*log2(5/14) - (9/14)*log2(9/14) = 0.9403
Next we compare it with the entropy computed after considering the split by looking at two child branches. In the left branch of ends-vowel=1, we have:
Entropy_left = - (3/7)*log2(3/7) - (4/7)*log2(4/7) = 0.9852
and the right branch of ends-vowel=0, we have:
Entropy_right = - (6/7)*log2(6/7) - (1/7)*log2(1/7) = 0.5917
We combine the left/right entropies using the number of instances down each branch asweight factor (7 instances went left, and 7 instances went right), and get the final entropy after the split:
Entropy_after = 7/14*Entropy_left + 7/14*Entropy_right = 0.7885
Now by comparing the entropy before and after the split, we obtain a measure ofinformation gain, or how much information we gained by doing the split using that particular feature:
Information_Gain = Entropy_before - Entropy_after = 0.1518
You can interpret the above calculation as following: by doing the split with the end-vowelsfeature, we were able to reduce uncertainty in the sub-tree prediction outcome by a small amount of 0.1518 (measured in bits as units of information).
At each node of the tree, this calculation is performed for every feature, and the feature with the largest information gain is chosen for the split in a greedy manner (thus favoring features that produce pure splits with low uncertainty/entropy). This process is applied recursively from the root-node down, and stops when a leaf node contains instances all having the same class (no need to split it further).
Note that I skipped over some details which are beyond the scope of this post, including how to handle numeric features, missing values, overfitting and pruning trees, etc..