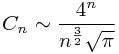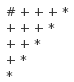杭电 hdu 1023——Train Problem II .
Description
Input
Output
Sample Input
1
2
3
10
Sample Output
1
2
5
16796
Hint
The result will be very large, so you may not process it by 32-bit integers.
1. 卡塔兰数的一般项公式为
4、
5、卡塔兰数的渐近增长为
它的含义是左式除以右式的商趋向于1当n → ∞。所有的奇卡塔兰数Cn都满足 。所有其他的卡塔兰数都是偶数。
卡特兰数的应用：
出栈次序
凸多边形三角划分
在一个 凸多边形 中，通过若干条互不相交的对角线，把这个多边形划分成了若 干个 三角形 。现在的任务是键盘上输入凸多边形的边数n，求不同划分的方案数f（n）。 比如当n=6时，f（6）=14。[6]
类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
给定N个节点，能构成多少种不同的二叉树？
，这一点很容易证明，我们考虑随便取一个节点作为根，那么他左边和右边的儿 子节点个数就确定了，假定根节点标号为x，那么左子树的标号就从1到x-1,共x-1个，右子树的标号就从x+1到n，共n-x个，那么我们的x从1取到n，就获得了所有的情况数
。这个式子就是我们性质3的式子。
种
n个非叶节点的满二叉树的形态数（对称后得到的二叉树除非自己本身对称，否则算是不同）
这里要求满二叉树，实际上就是在上一点的每个子节点的空儿子上都加上叶子，就形成了我们的图了，那么我们要求的结果就是Catalan数。
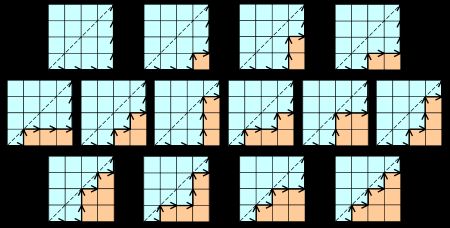
对于一个n*n的正方形网格，每次我们能向右或者向上移动一格，那么从左下角到右上角的所有在副对角线右下方的路径总数为。
我们将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列，我们所要保证的就是前k步中水平边的个数不小于垂直边的个数，换句话说前k个元素的和非负，就是我们关于Catalan数的定义。
凸n+2边形进行三角形分割（只连接顶点对形成n个三角形）数：
对于集合
的不交叉划分的数目为
这里解释一下不交叉划分，我们对于集合{a,b}和{c,d}，假设他们组成了两个区间[a,b]和[c,d]，我们假设两个区间不重合，那么以下四种情况当做是不交叉的：a<c<d<b，a<b<c<d，c<a<b<d与c<d<a<b，就是说两个区间可以包含或者相离，那么此时我们称集合{a,b}和{c,d}是不交叉的。对于集合，将里面元素两两分为一子集，共n个，若任意两个子集都是不交叉的，那么我们称此时的这个划分为一个不交叉划分。此时不交叉的划分数就是我们的了，证明也很容易，我们将每个子集中较小的数用左括号代替，较大的用右括号代替，那么带入原来的1至2n的序列中就形成了合法括号问题，就是我们第二点的结论。例如我们的集合{1,2,3,4,5,6}的不交叉划分有五个：{{1,2},{3,4},{5,6}}，{{1,2},{3,6},{4,5}}，{{1,4},{2,3},{5,6}}，{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。
。如下图所示：
这个证明是怎么进行的呢？我们先绘制如下的一张图片，即n为5的时候的阶梯：
我们注意到每个切割出来的矩形都必需包括一块标示为*的小正方形，那么我们此时枚举每个*与#标示的两角作为矩形，剩下的两个小阶梯就是我们的两个更小的子问题了，于是我们的
注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。
在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是。
平面上连接可以形成凸包的2n个点分成2个一组连成n条线段，两两线段之间不相交的情况总数是。
ｈ( n ) = ( ( 4*n-2 )/( n+1 )*h( n-1 ) );
*******************************
打表卡特兰数
第 n个 卡特兰数存在a[n]中，a[n][0]表示长度；
注意数是倒着存的，个位是 a[n][1] 输出时注意倒过来。
*********************************
#include <iostream>
using namespace std;
int a[101][101];
void get()
{
a[1][0]=1; a[1][1]=1;
a[2][0]=1; a[2][1]=2;
int i,j,sum=0,len=1;
for(i=3;i<=100;i++)
{
sum=0;
for(j=1;j<=len;j++) //乘法运算h（n-1）*（4*n-2）
{
int t=(a[i-1][j])*(4*i-2)+sum;
sum=t/10;
a[i][j]=t%10;
}
while(sum)
{
a[i][++len]=sum%10;
sum=sum/10;
}
for(j=len;j>=1;j--) //除法运算，除以分母的n+1
{
int t=a[i][j]+sum*10;
a[i][j]=t/(i+1);
sum=t%(i+1);
}
while(a[i][len]==0)
len--;
a[i][0]=len;
}
}
int main()
{
get();
int n;
while(cin>>n)
{
for(int i=a[n][0];i>=1;i--)
cout<<a[n][i];
cout<<endl;
}
return 0;
}