强连通分量算法Kosaraju 和 Tarjan
Kosaraju算法
对每个不在树中的点开始DFS一次,并记录离开各点的时间,这里是离开的时间,而不是到达时的,比如有图1->2 2->3 则1,2,3分别对应的时间是3 2 1,因为3没有出边,所以最先离开,其次是2,最后是1,
DFS后,在同一棵树中的点,如果dfn[v]>dfn[u]则说明点从v有可能到达u,而这棵树中的dfn[]最大的点,肯定可以到达每个点,从而在原图的逆图中,每次都选没有访问过的最大的dfn值开始DFS,如果可达点x 则说明它们是强连通的
void DFS_T(int u) {
int i,v;
if(used[u])return ;
used[u]=1;
id[u]=scc;
for(i=q[u]; i!=-1; i=Tedge[i].pre) { //注:存边的方式:前向星。
v=Tedge[i].d;
if(!used[v]) DFS_T(v);
}
}
void DFS(int v) {
int i,u;
if(used[v])return ;
used[v]=1;
for(i=p[v]; i!=-1; i=edge[i].pre) {
u=edge[i].d;
if(!used[u]) DFS(u);
}
order[++num]=v;
}
int Kosaraju() {
int i,j,k,v,u;
memset(used,0,sizeof(used));
num=0;
for(i=1; i<=n; ++i) if(!used[i]) DFS(i);
memset(used,0,sizeof(used));
memset(id,0,sizeof(id));
scc=0;
for(i=num; i>=1; --i) if(!used[order[i]]) scc++, DFS_T(order[i]);
}
Tarjan算法
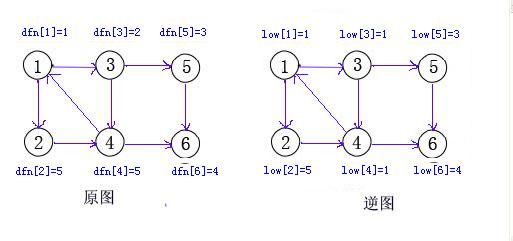
dfn[v]记录到达点v的时间,跟上面的离开不同,low[v]表示通过它的子结点可以到达的所有点中时间最小值,即low[i]=min(low[i],low[u]),u为v的了孙,初始化时low[v]=dfn[u]。如果low[v]比dfn[v]小,说明v可以通过它的子结点u,u1,u2...到达它的祖先v',则存在环,这个环上所有的点组成的子图便是一个强连通分量。换一个角度看,如果当low[v]==dfn[v]时,则它的子树中所有low[u]==dfn[v]的点都与v构成一个环,维护一个栈,DFS过程中,每遍历一个点则把它放入栈中,当发现low[v]==dfn[v]则依次把栈里的元素都弹出来,当栈顶元素为v时结束,这些点便构成一个以v为树根的强连通分量。
仍以上图为例,首先遍历点1,并dfn[1]=low[1]=++num, num表示按先后访问时间编号 ,同时1入栈
a.从3深入 dfn[3]=low[3]=2; 3入栈
b.从3到5 dfn[5]=low[5]=3; 5入栈
c.从5到6 dfn[6]=low[6]=4; 6入栈
d.发现6没有子结点可走,这时判断dfn[6]==low[6],于是开始弹栈,当遇到6时则break,即共弹出一个元素,于是6便是一个强连通分量
e.回溯至5,同样判断和弹栈,发现5也是一个强连通分量
f.再回溯至3,发现有边3->4,dfn[4]=low[4]=5,4入栈
g.4有边到1,由于1已经在栈里面,所以用dfn[1]更新low[4] 即low[4]=min(low[4],dfn[1])=1
h.回溯更新4的父亲3的low值 low[3]=min(low[3],low[4])=1
i.再回溯至1,发现有边1->2 继续深度遍历,2入栈,发现它的子结点4已经在栈中,直接更新low[2]=min(low[2],dfn[4]);
j.回溯至1,从而1所有出发的边都走了一遍,这时再比较low[1]与dfn[1],发现相等,于是开始弹栈,找到2,4,3,1这四个元素,构成一个连通分量。
void Tarjan(int v) {
dfn[v]=low[v]=++num;
used[v]=1;
st[++numSt]=v;
for(int i=p[v]; i!=-1; i=edge[i].pre) {
int u(edge[i].d);
if(!dfn[u]) { //还没有标号的点
Tarjan(u);//先遍历它的子结点
GetMin(low[v],low[u]);//用子结点更新当前点的low值
} else if(used[u]&&GetMin(low[v],dfn[u]));
}
if(dfn[v]==low[v]) {
scc++;
while(1) {
int u(st[numSt--]);
id[u]=scc;
used[u]=0;
if(v==u)break;
}
}
}
int main() {
for(int i=1; i<=n; ++i)
if(!dfn[i]) Tarjan(i);
}
这里有一个疑问,为什么当发现一个点v的子结点u已经在栈中时用dfn[u]来更新low[v],而不是用low[u],感觉好象两个都可以用,因为只要保证low[v]尽可能变小就行了