有趣的GOOGLE面试题

白话经典算法系列之十 一道有趣的GOOGLE面试题

分类： 白话经典算法系列 2012-11-21 09:03  12366人阅读  评论(58)  收藏  举报

白话经典算法 GOOGLE面试题 谷歌面试题 基数排序 哈希表

微博http://weibo.com/MoreWindows已开通，欢迎关注。

最近在微博上看到一道有趣的GOOGLE面试题，见下图：

文字版：

一个大小为n的数组，里面的数都属于范围[0, n-1]，有不确定的重复元素，找到至少一个重复元素，要求O(1)空间和O(n)时间。

 

    这个题目要求用O(n)的时间复杂度，这意味着只能遍历数组一次。同时还要寻找重复元素，很容易想到建立哈希表来完成，遍历数组时将每个元素映射到哈希表中，如果哈希表中已经存在这个元素则说明这就是个重复元素。因此直接使用C++ STL中的hash_set（参见《STL系列之六 set与hash_set》）可以方便的在O(n)时间内完成对重复元素的查找。

    但是题目却在空间复杂度上有限制——要求为O(1)的空间。因此采用哈希表这种解法肯定在空间复杂度上是不符合要求的。但可以沿着哈希法的思路继续思考，题目中数组中所以数字都在范围[0， n-1]，因此哈希表的大小为n即可。因此我们实际要做的就是对n个范围为0到n-1的数进行哈希，而哈希表的大小刚好为n。对排序算法比较熟悉的同学不难发现这与一种经典的排序算法——基数排序非常类似。而基数排序的时间空间复杂度刚好符合题目要求！因此尝试使用基数排序来解这道面试题。

 

    下面以2，4，1，5，7，6，1，9，0，2这十个数为例，展示下如何用基数排序来查找重复元素。

下标	0	1	2	3	4	5	6	7	8	9
数据	2	4	1	5	7	6	1	9	0	2

（1）由于第0个元素a[0] 等于2不为0，故交换a[0]与a[a[0]]即交换a[0]与a[2]得：

下标	0	1	2	3	4	5	6	7	8	9
数据	1	4	2	5	7	6	1	9	0	2

（2）由于第0个元素a[0] 等于1不为0，故交换a[0]与a[a[0]]即交换a[0]与a[1]得：

下标	0	1	2	3	4	5	6	7	8	9
数据	4	1	2	5	7	6	1	9	0	2

（3）由于第0个元素a[0] 等于4不为0，故交换a[0]与a[a[0]]即交换a[0]与a[4]得：

下标	0	1	2	3	4	5	6	7	8	9
数据	7	1	2	5	4	6	1	9	0	2

（4）由于第0个元素a[0] 等于7不为0，故交换a[0]与a[a[0]]即交换a[0]与a[7]得：

下标	0	1	2	3	4	5	6	7	8	9
数据	9	1	2	5	4	6	1	7	0	2

（5）由于第0个元素a[0] 等于9不为0，故交换a[0]与a[a[0]]即交换a[0]与a[9]得：

下标	0	1	2	3	4	5	6	7	8	9
数据	2	1	2	5	4	6	1	7	0	9

（6）由于第0个元素a[0] 等于2不为0，故交换a[0]与a[a[0]]即交换a[0]与a[2]，但a[2]也为2与a[0]相等，因此我们就找到了一个重复的元素——2。

下标	0	1	2	3	4	5	6	7	8	9
数据	2	1	2	5	4	6	1	7	0	9

 

 

    有了上面的分析，代码不难写出：

 //GOOGLE面试题
 //一个大小为n的数组，里面的数都属于范围[0, n-1]，有不确定的重复元素，找到至少一个重复元素，要求O(1)空间和O(n)时间。
 //By MoreWindows (http://blog.csdn.net/MoreWindows)
 #include <stdio.h>
 const int NO_REPEAT_FLAG = -1;
 void Swap(int &x, int &y)
 {
     int t = x;
     x = y;
     y = t;
 }
 //类似于基数排序，找出数组中第一个重复元素。
 int RadixSort(int a[], int n)
 {
     int i;
     for (i = 0; i < n; i++)
     {
         while (i != a[i])
         {
             if (a[i] == a[a[i]])
                 return a[i];
             Swap(a[i], a[a[i]]);
         }
     }
     return NO_REPEAT_FLAG;
 }
 void PrintfArray(int a[], int n)
 {
     for (int i = 0; i < n; i++)
         printf("%d ", a[i]);
     putchar('\n');
 }
 int main()
 {
     printf("    白话经典算法系列之十 一道有趣的GOOGLE面试题 \n");
     printf(" -- by MoreWindows( http://blog.csdn.net/MoreWindows ) --\n\n");

     const int MAXN = 10;
     int a[MAXN] = {2, 4, 1, 5, 7,  6, 1, 9, 0, 2};
     //int a[MAXN] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};

     printf("数组为: \n");
     PrintfArray(a, MAXN);

     int nRepeatNumber = RadixSort(a, MAXN);
     if (nRepeatNumber != NO_REPEAT_FLAG)
         printf("该数组有重复元素，此元素为%d\n", nRepeatNumber);
     else
         printf("该数组没有重复元素\n");
     return 0;
 }

    运行结果如下图所示：

    整个程序的核心代码只有短短5行左右，虽然有二重循环语句，但每个元素只会被访问一次，完成符合题目对时间复杂度的要求。

 

用基数排序来解决这道题目虽然思维巧妙，但会改动原数组的数据。有没有一种解法既找出一个重复的数据，又不改动数组中的数据了？请看《【白话经典算法系列之十一】一道有趣的GOOGLE面试题 --【解法2】》。

 

 

转载请标明出处，原文地址：http://blog.csdn.net/morewindows/article/details/8204460

欢迎关注微博：http://weibo.com/MoreWindows

另外，白话经典算法系列的电子书已经发布至第二版了，下载地址为：http://download.csdn.net/detail/morewindows/4560056

 

 

【白话经典算法系列之十二】数组中只出现1次的两个数字(百度面试题) 将介绍一道百度面试题，欢迎大家浏览。

 

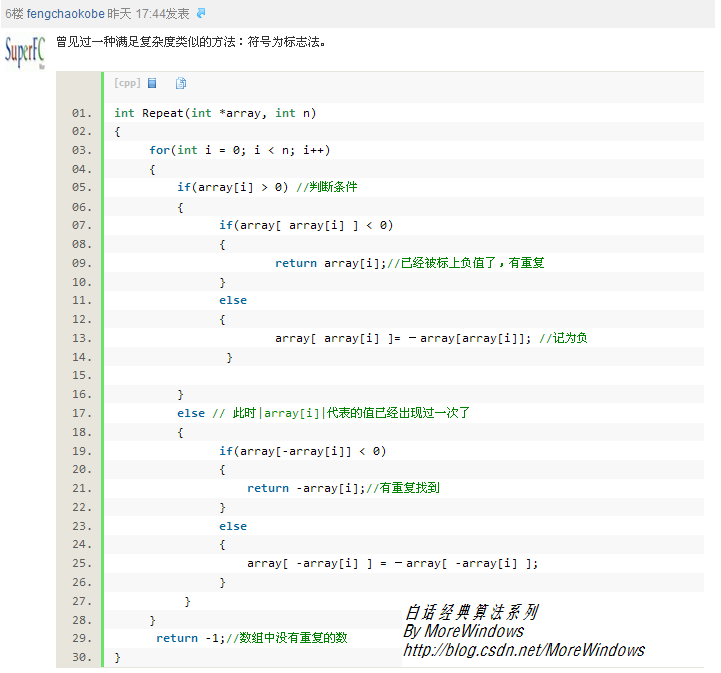
 上一篇《白话经典算法系列之十一道有趣的GOOGLE面试题》中对一道有趣的GOOGLE面试题进行了详细的讲解，使用了类似于基数排序的做法在O(N)的时间复杂度和O(1)的空间复杂度完成了题目的要求，文章发表后，网友fengchaokobe在评论中给出了另一种解法，见下图。

文字版：

 int Repeat(int *a, int n)
 {
     for(int i = 0; i < n; i++)
     {
         if(a[i] > 0) //判断条件
         {
             if(a[ a[i] ] < 0)
             {
                 return a[i];//已经被标上负值了，有重复
             }
             else
             {
                 a[ a[i] ]= -a[a[i]]; //记为负
             }

         }
         else // 此时|a[i]|代表的值已经出现过一次了
         {
             if(a[-a[i]] < 0)
             {
                 return -a[i];//有重复找到
             }
             else
             {
                 a[ -a[i] ] = -a[ -a[i] ];
             }
         }
     }
     return -1;//数组中没有重复的数
 }

下面对这种以取负为访问标志的方法用个实例来说明下：

    设int a[] = {1, 2, 1}

    第一步：由于a[0]等于1大于0，因此先判断下a[a[0]]即a[1]是否小于0，如果小于，说明这是第二次访问下标为1的元素，表明我们已经找到了重复元素。不是则将a[a[0]]取负，a[1]=-a[1]=-2。

    第二步：由于a[1]等于-2，因此先判断下a[-a[1]]取出a[2]是否小于0，如果小于，说明这是第二次访问下标为2的元素，表明我们已经找到了重复元素。不是则将a[-a[1]]取负，a[2]=-a[2]=-1。

    第三步：由于a[2]等于-1，因此判断下a[-a[2]]即a[1]是否小于0，由于a[1]在第一步中被取反过了，因此证明这是第二次访问下标为1的元素，直接返回-a[2]即可。

 

这种通过取负来判断元素是否重复访问的方法正如网友jwfeng002所言，当数组第0个元素为0且数据中只有0重复时是无法找出正确解的。只要用：

       const int MAXN = 5;

       int a[MAXN] = {0, 1, 2, 3, 0};

这组数据来测试，就会发现该方法无法判断0是个重复出现的元素。运行结果如下图所示：

 

这个算法虽然有缺陷，但我们可以沿着这个算法的思路——这个算法之所以用到了取负，是因此根据题目条件，数组中数据范围为[0，n-1]，因此可以通过判断元素是否大于0来决定这个元素是未访问过的数据还是已访问过的数据。但也正因为对0的取负是无效操作决定了这个算法存在着缺陷。要改进一下也很简单——不用取负，而用加n。这样通过判断元素是否大于等于n就能决定这个元素是未访问过的数据还是已访问过的数据。完整代码如下：

 //GOOGLE面试题
 //一个大小为n的数组，里面的数都属于范围[0, n-1]，有不确定的重复元素，找到至少一个重复元素，要求O(1)空间和O(n)时间。
 //By MoreWindows (http://blog.csdn.net/MoreWindows)
 #include <stdio.h>
 const int NO_REPEAT_FLAG = -1;
 int FindRepeatNumberInArray(int *a, int n)
 {
     for(int i = 0; i < n; i++)
     {
         int nRealIndex = a[i] >= n ? a[i] - n : a[i];
         if (a[nRealIndex] >= n) //这个位置上的值大于n说明已经是第二次访问这个位置了
             return nRealIndex;
         else
             a[nRealIndex] += n;
     }
     return NO_REPEAT_FLAG; //数组中没有重复的数
 }
 void PrintfArray(int a[], int n)
 {
     for (int i = 0; i < n; i++)
         printf("%d ", a[i]);
     putchar('\n');
 }
 int main()
 {
     printf("    白话经典算法系列之十一 一道有趣的GOOGLE面试题解法2\n");
     printf(" -- by MoreWindows( http://blog.csdn.net/MoreWindows ) --\n\n");

     const int MAXN = 10;
     //int a[MAXN] = {2, 4, 1, 5, 7,  6, 1, 9, 0, 2};
     int a[MAXN] = {0, 1, 2, 3, 4,  5, 6, 7, 8, 0};

     printf("数组为: \n");
     PrintfArray(a, MAXN);

     int nRepeatNumber = FindRepeatNumberInArray(a, MAXN);
     if (nRepeatNumber != NO_REPEAT_FLAG)
         printf("该数组有重复元素，此元素为%d\n", nRepeatNumber);
     else
         printf("该数组没有重复元素\n");
     return 0;
 }

运行结果如图所示：

如同上一篇《白话经典算法系列之十一道有趣的GOOGLE面试题》一样，算法的核心代码依然只有短短5行左右。在时间空间复杂度上也同样满足题目要求。

 

 

相信由这篇文章可以看出，思维的转换性对寻找一个合适算法是非常有用的。

 

另外，代码的书写也要注意一下，对比一下文章中的Repeat()函数与FindRepeatNumberInArray()就能发现对代码进行一下简洁是非常有必要的。如果真在GOOGLE的面试中，虽然都完成了面试题，但面试官对这二份代码的感觉会是如何了？这也正是很多童鞋在面试后感觉困惑，为什么答的还不错怎么就面挂了。

 

白话经典算法系列文章地址：

http://blog.csdn.net/MoreWindows/article/category/859207

转载请标明出处，原文地址：http://blog.csdn.net/morewindows/article/details/8212446

欢迎关注微博：http://weibo.com/MoreWindows