BZOJ 1502 NOI 2005 月下柠檬树 计算几何 自适应辛普森积分
题目大意:有一个由圆锥和圆台组成的柠檬树,在月亮发出的平行光下,可以形成一个影子,求这个影子的面积。
思路:理解投影的性质:只要是平行光线,投影在水平面上,所得的图形都与原图形全等。
知道了这一点我们就可以画画图,分析就知道,其实柠檬树的影子,就是一些园和等腰梯形的面积的并。(如下图,样例)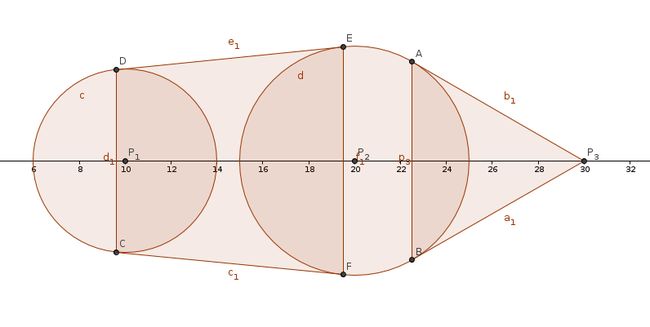
运用计算几何的知识就可以得到圆的方程和圆的公切线的方程,然后得到一个连续的函数。最后这个题就成为一直函数的解析式,求这个函数与X轴之间的面积。
套用辛普森积分:Simpson(l,r) = (F(l) + F(r) + F(mid) * 4) * (r - l) / 6.0,然后递归检查精度,如果左值+右值-总值的绝对值小于精度就返回,否则就递归返回左侧面积和右侧面积。得到一个近似精确的值就是所求的答案。
CODE:
#include <cmath>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <iostream>
#include <algorithm>
#define MAX 10000
#define EPS 1e-6
#define INF 0x7f7f7f7f
using namespace std;
struct Circle{
double length,r;
}circle[MAX];
struct Line{
double k,b;
double st,ed;
}line[MAX];
int cnt;
double alpha,start,end;
int lines;
double temp;
double GetArea(double l,double r,double _area);
double Simpson(double l,double r);
double F(double x);
int main()
{
cin >> cnt >> alpha;
alpha = 1.0 / tan(alpha);
cnt++;
for(int i = 1;i <= cnt; ++i) {
scanf("%lf",&temp);
circle[i].length = circle[i - 1].length + temp * alpha;
}
for(int i = 1;i <= cnt; ++i)
for(int j = i + 1;j <= cnt; ++j) {
}
start = end = circle[cnt].length;
for(int i = 1;i < cnt; ++i) {
scanf("%lf",&circle[i].r);
start = min(start,circle[i].length - circle[i].r);
end = max(end,circle[i].length + circle[i].r);
}
for(int i = 1;i < cnt; ++i) {
if(circle[i + 1].length - circle[i].length - fabs(circle[i + 1].r - circle[i].r) < EPS)
continue;
double sin_a = (circle[i + 1].r - circle[i].r) / (circle[i + 1].length - circle[i].length);
double cos_a = sqrt(1.0 - sin_a * sin_a);
double tan_a = sin_a / cos_a;
Line *l = &line[++lines];
l->st = circle[i].length - circle[i].r * sin_a;
l->ed = circle[i + 1].length - circle[i + 1].r * sin_a;
l->k = tan_a;
l->b = circle[i].r * cos_a - l->st * tan_a;
}
cout << fixed << setprecision(2) << 2.0 * GetArea(start,end,Simpson(start,end)) << endl;
return 0;
}
double GetArea(double l,double r,double _area)
{
double mid = (l + r) / 2.0;
double l_area = Simpson(l,mid),r_area = Simpson(mid,r);
if(fabs(l_area + r_area - _area) < EPS)
return _area;
return GetArea(l,mid,l_area) + GetArea(mid,r,r_area);
}
double Simpson(double l,double r)
{
double mid = (l + r) / 2.0;
return (F(l) + 4.0 * F(mid) + F(r)) * (r - l) / 6.0;
}
double F(double x)
{
double re = 0.0;
for(int i = 1;i <= lines; ++i)
if(x <= line[i].ed && x >= line[i].st)
re = max(re,line[i].k * x + line[i].b);
for(int i = 1;i <= cnt; ++i)
if(x <= circle[i].length + circle[i].r && x >= circle[i].length - circle[i].r)
re = max(re,sqrt(circle[i].r * circle[i].r - (circle[i].length - x) * (circle[i].length - x)));
return re;
}