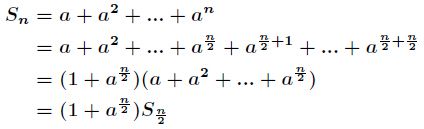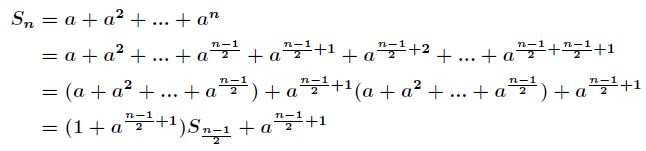POJ 3233 - Matrix Power Series(等比矩阵求和)
题意:矩阵求和![]()
思路:用二分幂解决,和等比数列求和的二分方法一样
等比数列求和法(摘自http://blog.csdn.net/acdreamers/article/details/7851144 ACdreams)
有效地求表达式![]() 的值:
的值:
(1)当![]() 时,
时,![]()
(2)当![]() 时,那么有
时,那么有
(3)当![]() 时,那么有
时,那么有
//888K 594MS C++ 1627B
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 35;
struct mat
{
int a[MAXN][MAXN];
mat()
{
memset(a,0,sizeof(a));
}
};
mat m;
mat I;
int n,k,mod;
mat add(mat m1,mat m2)
{
mat ans;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans.a[i][j]=(m1.a[i][j]+m2.a[i][j])%mod;
return ans;
}
mat mul(mat m1,mat m2)
{
mat ans;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(m1.a[i][j])
for(int k=1;k<=n;k++)
ans.a[i][k]=(ans.a[i][k]+m1.a[i][j]*m2.a[j][k])%mod;
return ans;
}
mat quickmul(mat m,int k)
{
mat ans;
for(int i=1;i<=n;i++) ans.a[i][i] = 1;
while(k)
{
if(k&1) ans=mul(ans,m);
m=mul(m,m);
k>>=1;
}
return ans;
}
mat sum(int k)//等比求和
{
if(k==1) return m;
mat t=sum(k/2);
mat ans;
if(k&1)
{
mat cur=quickmul(m,k/2+1);
ans=add(mul(add(I,cur),t),cur);
}
else
{
mat cur=quickmul(m,k/2);
ans=mul(add(I,cur),t);
}
return ans;
}
void print(mat m)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
printf("%d%c",m.a[i][j],j==n? '\n':' ');
}
int main()
{
while(~scanf("%d%d%d",&n,&k,&mod))
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
scanf("%d",&m.a[i][j]);
I.a[i][j]=(i==j);
}
mat ans=sum(k);
print(ans);
}
return 0;
}