UVA 10652 Board Wrapping (凸包面积)
|
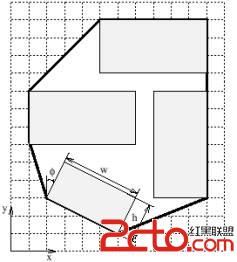
InputOn the first line of input there is one integer, N <= 50, giving the number of test cases (moulds) in the input. After this line, N test cases follow. Each test case starts with a line containing one integer n, 1< n <= 600, which is the number of boards in the mould. Then n lines follow, each with five floating point numbers x, y, w, h, j where 0 <= x, y, w, h <=10000 and –90° < j <=90°. The x and y are the coordinates of the center of the board and w and h are the width and height of the board, respectively. j is the angle between the height axis of the board to the y-axis in degrees, positive clockwise. That is, if j = 0, the projection of the board on the x-axis would be w. Of course, the boards cannot intersect.
OutputFor every test case, output one line containing the fraction of the space occupied by the boards to the total space in percent. Your output should have one decimal digit and be followed by a space and a percent sign (%).
|
| 1 4 4 7.5 6 3 0 8 11.5 6 3 0 9.5 6 6 3 90 4.5 3 4.4721 2.2361 26.565 |
64.3 %
|
题意:有n个木板,用面积尽量小的凸多边形把他们包起来,并计算出木板占整个包装面积的百分比。第一行一个数据组数T,每组数据第一行一个木板个数n,以下n行每行5个实数 x, y, w, h, j (0<=x,y,w,h<=10000 -90<=j<=90) ,其中(x,y)是木板中心的坐标,w是宽,h是高,j是顺时针旋转的角度(j=0表示不旋转,此时长度为w的那条边应该是水平方向)。木板保证互不相交。对于每组数据输出木板总面积占包装面积的百分比,保留小数点后1位
#include <iostream>
#include <algorithm>
#include <math.h>
#include <iomanip>
using namespace std;
struct Point
{
double x,y;
Point(){}
Point(double x,double y):x(x),y(y){}
} ;
bool operator < (const Point&a,const Point&b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
Point operator+(Point A,Point B)
{
return Point(A.x+B.x,A.y+B.y);
}
Point operator-(Point A,Point B)
{
return Point(A.x-B.x,A.y-B.y);
}
double torad(double deg)//角度转换为弧度
{
return deg/180*acos(-1);
}
Point Rotate(Point A,double rad)//向量旋转
{
return Point(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double Cross(Point A,Point B)
{
return A.x*B.y-A.y*B.x;
}
double PolygonArea(Point *p,int n)
{
double area=0;
for(int i=1;i<n-1;i++)
area=area+Cross(p[i]-p[0],p[i+1]-p[0]);
return area/2;
}
int ConvexHull(Point *p,int n,Point *ch)
{
sort(p,p+n);
int m=0;
for(int i=0;i<n;i++)
{
while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
ch[m++]=p[i];
}
int k=m;
for(int i=n-2;i>=0;i--)
{
while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
ch[m++]=p[i];
}
if(n>1)m--;
return m;
}
int main()
{
int T;
cin>>T;
while(T--)
{
int N,t=0;
Point P[2500],ch[2500];
cin>>N;
double area=0;
for(int i=0;i<N;i++)
{
double x,y,w,h,j;
cin>>x>>y>>w>>h>>j;
Point o(x,y);
double ang=-torad(j);//顺时针旋转
P[t++]=o+Rotate(Point(-w/2,-h/2),ang); //求所给的长方形木板的四个顶点
P[t++]=o+Rotate(Point(w/2,-h/2),ang);
P[t++]=o+Rotate(Point(-w/2,h/2),ang);
P[t++]=o+Rotate(Point(w/2,h/2),ang);
area=area+w*h;//累加木板总面积
}
int m=ConvexHull(P,t,ch);
double area2=PolygonArea(ch,m);
cout<<setiosflags(ios::fixed)<<setprecision(1);
cout<<area*100/area2<<" %"<<endl;
}
return 0;
}