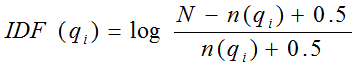Coreseek算法分析(转)
Coreseek算法分析
本文对coreseek代码中涉及到的一部分算法进行说明,以便在阅读代码的时候,能更容易理解相关的代码。本文所整理的只是其中的部分算法,后面将在逐渐深入理解的基础上,进一步添加。
一.Soundex 算法
1. 算法原理
Soundex是一种语音算法,利用英文字的读音计算近似值,值由四个字符构成,第一个字符为英文字母,后三个为数字。在拼音文字中有时会有会念但不能拼出正确字的情形,可用Soundex做类似模糊匹配的效果。例如Knuth和Kant二个字符串,它们的Soundex值都是 K530。
大部分的数据库服务器都有 Soundex 函数。Soundex 算法有几个差别不大的变化版本。更详细的说明参考Donald Knuth大师的名著:电脑程序设计的艺术 (The Art Of Computer Programming) 第三卷排序和搜寻。
1 名字的第一个字母不变。
2 根据特定的对照表,将剩下的字母转换为数字:
u a e h i o u w y -> 0
u b f p v -> 1
u c g j k q s x z -> 2
u d t -> 3
u l -> 4
u m n -> 5
u r -> 6
3 去除连续重复。
4 去除所有 9。
5 如果结果都少于四个字符 (第一个字母加上后面的三位字符),就以零补齐。
6 如果结果超过四个字符,丢弃掉四位之后的字符。
以Knuth和Kant为例:
Knuth -> K5030 -> K53 -> K530
Kant -> K053 -> K53 -> K530
2.算法实现
Sphinxsoundex.cpp文件中的void stem_soundex ( BYTE * pWord )函数实现。
void stem_soundex ( BYTE * pWord )
{
// 字母转化规则用数组表示,后面直接根据数组进行映射转化
static BYTE dLetter2Code [ 27 ] = "01230120022455012623010202";
// check if the word only contains lowercase English letters
BYTE * p = pWord;
// 进行非英语字母的过滤
while ( *p>='a' && *p<='z' )
p++;
if ( *p )
return;
// do soundex
p = pWord+1;
BYTE * pOut = pWord+1;
while ( *p )
{
// 对每一个字符,根据映射关系进行转化,得到转化以后的编码值。
BYTE c = dLetter2Code [ (*p)-'a' ];
if ( c!='0' && pOut[-1]!=c )
*pOut++ = c;
p++;
}
// 补0的操作
while ( pOut-pWord<4 && pOut<p )
*pOut++ = '0';
*pOut++ = '/0';
}
二.Metaphone算法
1. 算法原理
Metaphone是一种基于发音的算法,跟传统的soundex算法相比,metaphone是产生可变长度的输出作为编码值,而soundex是产生固定长度的输出。发音相似的词语产生相同的输出。
Metaphone算法是为了客服soundex算法的一些缺点而发展出来的,它使用了大量的英语发音规则作为算法的依据。后来逐渐有一些算法的变种出现,比如double metaphone算法和Metaphone 3算法。
Metaphone编码算法采用16个常数符号:0BFHJKLMNPRSTWXY。用'0'表示 "th" , 'X' 表示"sh" 或 "ch", 其他的符号用来表示他们各自在英语中的发音。元音AEIOU也被用来编码,但值在一个编码的开头使用。下面是这个编码的编码规则。
1. Drop duplicate adjacent letters, except for C.
2. If the word begins with 'KN', 'GN', 'PN', 'AE', 'WR', drop the first letter.
3. Drop 'B' if after 'M' and if it is at the end of the word.
4. 'C' transforms to 'X' if followed by 'IA' or 'H' (unless in latter case, it is part of '-SCH-', in which case it transforms to 'K'). 'C' transforms to 'S' if followed by 'I', 'E', or 'Y'. Otherwise, 'C' transforms to 'K'.
5. 'D' transforms to 'J' if followed by 'GE', 'GY', or 'GI'. Otherwise, 'D' transforms to 'T'.
6. Drop 'G' if followed by 'H' and 'H' is not at the end or before a vowel. Drop 'G' if followed by 'N' or 'NED' and is at the end.
7. 'G' transforms to 'J' if before 'I', 'E', or 'Y', and it is not in 'GG'. Otherwise, 'G' transforms to 'K'. Reduce 'GG' to 'G'.
8. Drop 'H' if after vowel and not before a vowel.
9. 'CK' transforms to 'K'.
10. 'PH' transforms to 'F'.
11. 'Q' transforms to 'K'.
12. 'S' transforms to 'X' if followed by 'H', 'IO', or 'IA'.
13. 'T' transforms to 'X' if followed by 'IA' or 'IO'. 'TH' transforms to '0'. Drop 'T' if followed by 'CH'.
14. 'V' transforms to 'F'.
15. 'WH' transforms to 'W' if at the beginning. Drop 'W' if not followed by a vowel.
16. 'X' transforms to 'S' if at the beginning. Otherwise, 'X' transforms to 'KS'.
17. Drop 'Y' if not followed by a vowel.
18. 'Z' transforms to 'S'.
19. Drop all vowels unless it is the beginning.
2. 算法实现
在sphinxmetaphone.cpp文件中的void stem_dmetaphone ( BYTE * pWord, bool bUTF8 )函数中实现。
因为算法比较简单,跟soundex类似,主要是规则的转化,所以不再一一说明。
三. MMSEG 中文分词算法
1. MMSeg算法原理
要理解mmseg算法,首先来理解一下chunk,它是MMSeg分词算法中一个关键的概念。Chunk中包含依据上下文分出的一组词和相关的属性,包括长度(Length)、平均长度(Average Length)、标准差的平方(Variance)和自由语素度(Degree Of Morphemic Freedom)。下面列出了这4个属性:
| 属性 |
含义 |
| 长度(Length) |
chuck中各个词的长度之和 |
| 平均长度(Average Length) |
长度(Length)/词数 |
| 标准差的平方(Variance) |
同数学中的定义 |
| 自由语素度(Degree Of Morphemic Freedom) |
各单字词词频的对数之和 |
Chunk中的4个属性只有在需要该属性的值时才进行计算,而且只计算一次。
其次来理解一下规则(Rule),它是MMSeg分词算法中的又一个关键的概念。实际上我们可以将规则理解为一个过滤器(Filter),过滤掉不符合要求的chunk。MMSeg分词算法中涉及了4个规则:
· 规则1:取最大匹配的chunk (Rule 1: Maximum matching)
· 规则2:取平均词长最大的chunk (Rule 2: Largest average word length)
· 规则3:取词长标准差最小的chunk (Rule 3: Smallest variance of word lengths)
· 规则4:取单字词自由语素度之和最大的chunk (Rule 4: Largest sum of degree of morphemic freedom of one-character words)
这4个规则符合汉语成词的基本习惯。
再来理解一下匹配方式复杂最大匹配(Complex maximum matching):
复杂最大匹配先使用规则1来过滤chunks,如果过滤后的结果多于或等于2,则使用规则2继续过滤,否则终止过滤过程。如果使用规则2得到的过滤结果多于或等于2,则使用规则3继续过滤,否则终止过滤过程。如果使用规则3得到的过滤结果多于或等于2,则使用规则4继续过滤,否则终止过滤过程。如果使用规则 4得到的过滤结果多于或等于2,则抛出一个表示歧义的异常,否则终止过滤过程。
最后通过一个例句--“研究生命起源"来简述一下复杂最大匹配的分词过程。MMSeg分词算法会得到7个chunk,分别为:
| 编号 |
chunk |
长度 |
| 0 |
研_究_生 |
3 |
| 1 |
研_究_生命 |
4 |
| 2 |
研究_生_命 |
4 |
| 3 |
研究_生命_起 |
5 |
| 4 |
研究_生命_起源 |
6 |
| 5 |
研究生_命_起 |
5 |
| 6 |
研究生_命_起源 |
6 |
使用规则1过滤后得到2个chunk,如下:
| 编号 |
chunk |
长度 |
| 4 |
研究_生命_起源 |
6 |
| 6 |
研究生_命_起源 |
6 |
计算平均长度后为:
| 编号 |
chunk |
长度 |
平均长度 |
| 4 |
研究_生命_起源 |
6 |
2 |
| 6 |
研究生_命_起源 |
6 |
2 |
使用规则2过滤后得到2个chunk,如下:
| 编号 |
chunk |
长度 |
平均长度 |
| 4 |
研究_生命_起源 |
6 |
2 |
| 6 |
研究生_命_起源 |
6 |
2 |
计算标准差的平方后为:
| 编号 |
chunk |
长度 |
平均长度 |
标准差的平方 |
| 4 |
研究_生命_起源 |
6 |
2 |
0 |
| 6 |
研究生_命_起源 |
6 |
2 |
4/9 |
使用规则3过滤后得到1个chunk,如下:
| 编号 |
chunk |
长度 |
平均长度 |
标准差的平方 |
| 4 |
研究_生命_起源 |
6 |
2 |
0 |
匹配过程终止。最终取“研究”成词,以相同的方法继续处理“生命起源”。
分词效果:
研究_生命_起源_
研究生_教育_
2. MMSeg代码实现
在mmthunk.h文件中的 class ChunkQueue::getToken()函数中实现。
u2 getToken(){
size_t num_chunk = m_chunks.size();
if(!num_chunk)
return 0;
if(num_chunk == 1)
return m_chunks[0].tokens[0];
// 取平均词长最大的chunk (Rule 2: Largest average word length)
float avg_length = 0;
u4 remains[256]; //m_chunks.size can not larger than 256;
u4* k_ptr = remains;
for(size_t i = 0; i<m_chunks.size();i++){
float avl = m_chunks[i].get_avl();
if(avl > avg_length){
avg_length = avl;
k_ptr = remains;
*k_ptr = (u4)i;
k_ptr++;
}else
if(avl == avg_length){
*k_ptr = (u4)i;
k_ptr++;
}
}
if((k_ptr - remains) == 1)
return m_chunks[remains[0]].tokens[0]; //match by rule2
// 规则3:取词长标准差最小的chunk (Rule 3: Smallest variance of word lengths)
u4 remains_r3[256];
u4* k_ptr_r3 = remains_r3;
avg_length = 1024*64; //an unreachable avg
for(size_t i = 0; i<k_ptr-remains; i++){
float avg = m_chunks[remains[i]].get_avg();
if(avg < avg_length) {
avg_length = avg;
k_ptr_r3 = remains_r3;
*k_ptr_r3 = (u4)remains[i];//*k_ptr_r3 = (u4)i;
k_ptr_r3++;
}else
if(avg == avg_length){
*k_ptr_r3 = (u4)i;
k_ptr_r3++;
}
}
if((k_ptr_r3 - remains_r3) == 1)
return m_chunks[remains_r3[0]].tokens[0]; //match by rule3 min avg_length
// 规则4:取单字词自由语素度之和最大的chunk
// (Rule 4: Largest sum of degree of morphemic freedom of one-character words)
float max_score = 0.0;
size_t idx = -1;
for(size_t i = 0; i<k_ptr_r3-remains_r3; i++){
float score = m_chunks[remains_r3[i]].get_free();
if(score>max_score){
max_score = score;
idx = remains_r3[i];
}
}
return m_chunks[idx].tokens[0];
//return 0;
};
四. N-gram算法
1. 算法原理
N-gram是一种基于统计语言模型的算法。
统计语言模型的基本原理公式是:
假设一个句子S可以表示为一个序列S=w1w2…wn,语言模型就是要求句子S的概率P(S):
这个概率的计算量太大,解决问题的方法是将所有历史w1w2…wi-1按照某个规则映射到等价类S(w1w2…wi-1),等价类的数目远远小于不同历史的数目,即假定:
![]()
N-Gram模型
当两个历史的最近的N-1个词(或字)相同时,映射两个历史到同一个等价类,在此情况下的模型称之为N-Gram模型。
N-Gram模型实质是一种马尔科夫链。 N的值不能太大,否则计算仍然太大。
根据最大似然估计,语言模型的参数:
其中,C(w1w2…wi)表示w1w2…wi在训练数据中出现的次数
在分词中的应用
我们回到句子的概率计算公式:假设一个句子S可以表示为一个序列S=w1w2…wn,语言模型就是要求句子S的概率P(S):
对于中文来说,一个句子的序列划分有多种方式,
S=w1w2w3....wn
S = a1a2a3....ak
......等等
不同的划分计算出来的句子的概率是不一样的。我们把整个句子最大概率的划分方式作为第一个词的划分结果,然后分词窗口后移,继续下一步。
2. 程序代码
Ngram算法似乎没有实现,至少在中文分词中是没有实现,目前的ngram的n缺省是1, 在中文分词中是0。在sphinx很多代码中预留了这个ngram的选项,可能会在后面的版本中加入,也有可能是我目前没有看到这部分代码,可以在看新版本的代码中注意下。
在很多拼音输入法中,ngram算法用来做输入联想提示。在搜索中,也常用来做错误输入的纠正提示。
五. Bm25算法
1. 算法原理
BM25算法,通常用来作搜索相关性平分。一句话概况其主要思想:对Query进行语素解析,生成语素qi;然后,对于每个搜索结果D,计算每个语素qi与D的相关性得分,最后,将qi相对于D的相关性得分进行加权求和,从而得到Query与D的相关性得分。
BM25算法的一般性公式如下:
其中,Q表示Query,qi表示Q解析之后的一个语素(对中文而言,我们可以把对Query的分词作为语素分析,每个词看成语素qi。);d表示一个搜索结果文档;Wi表示语素qi的权重;R(qi,d)表示语素qi与文档d的相关性得分。
下面我们来看如何定义Wi。判断一个词与一个文档的相关性的权重,方法有多种,较常用的是IDF。这里以IDF为例,公式如下:
其中,N为索引中的全部文档数,n(qi)为包含了qi的文档数。
根据IDF的定义可以看出,对于给定的文档集合,包含了qi的文档数越多,qi的权重则越低。也就是说,当很多文档都包含了qi时,qi的区分度就不高,因此使用qi来判断相关性时的重要度就较低。
我们再来看语素qi与文档d的相关性得分R(qi,d)。首先来看BM25中相关性得分的一般形式:
其中,k1,k2,b为调节因子,通常根据经验设置,一般k1=2,b=0.75;fi为qi在d中的出现频率,qfi为qi在Query中的出现频率。dl为文档d的长度,avgdl为所有文档的平均长度。由于绝大部分情况下,qi在Query中只会出现一次,即qfi=1,因此公式可以简化为:
从K的定义中可以看到,参数b的作用是调整文档长度对相关性影响的大小。b越大,文档长度的对相关性得分的影响越大,反之越小。而文档的相对长度越长,K值将越大,则相关性得分会越小。这可以理解为,当文档较长时,包含qi的机会越大,因此,同等fi的情况下,长文档与qi的相关性应该比短文档与qi的相关性弱。
综上,BM25算法的相关性得分公式可总结为:
从BM25的公式可以看到,通过使用不同的语素分析方法、语素权重判定方法,以及语素与文档的相关性判定方法,我们可以衍生出不同的搜索相关性得分计算方法,这就为我们设计算法提供了较大的灵活性。
2. 代码实现
算法的实现在下面这个函数里卖呢,但程序中的算法已经很弱化了。已经没有bm25算法的本质思想了,更像最佳匹配算法。
int ExtRanker_BM25_c::GetMatches ( int iFields, const int * pWeights )
{
if ( !m_pRoot )
return 0;
const ExtDoc_t * pDoc = m_pDoclist;
int iMatches = 0;
while ( iMatches<ExtNode_i::MAX_DOCS )
{
if ( !pDoc || pDoc->m_uDocid==DOCID_MAX ) pDoc = GetFilteredDocs ();
if ( !pDoc ) { m_pDoclist = NULL; return iMatches; }
DWORD uRank = 0;
//m_uFields:current match fields,每一bit代表一个查询词是否在文档中出现,
// 因此在一次查询中,最多32个查询词
// 文档中匹配的每一个查询词,乘于这个查询词的权重,用来计算文档的权重。
// bm25算法的严重弱化,只把查询词出现的次数乘于权重来计算文档的权重
for ( int i=0; i<iFields; i++ )
uRank += ( (pDoc->m_uFields>>i)&1 )*pWeights[i];
// m_dMatches:top matching documents, no more than MAX_MATCHES
// m_dMyMatches: my local matches pool; for filtering
Swap ( m_dMatches[iMatches], m_dMyMatches[pDoc-m_dMyDocs] ); // OPTIMIZE? can avoid this swap and simply return m_dMyMatches (though in lesser chunks)
m_dMatches[iMatches].m_iWeight += uRank*SPH_BM25_SCALE;
iMatches++;
pDoc++;
}
m_pDoclist = pDoc;
return iMatches;
}
六. stemming 算法
1. 算法原理
所谓stemming算法,又叫做词干抽取算法。是依据英语中的语法规则,将一些类似的单词,映射成为相同的单词。比如 CONNECT,CONNECTED
,CONNECTING,CONNECTION,CONNECTIONS这些单词,含义都类似,都可以转化成connect。查找connect的时候,应该把这些都查找出来。
Sphinx的stemming算法采用了snowball项目中的stemming算法,跟经典的porter stemming算法基本一样。
Stemming算法和前面说明的 “soundex”和“metaphone"。算法一样,都是一种转型算法。不过它的转化规则更多更繁琐,具体可以参照porter stemmer的算法论文,不再进行翻译了。http://snowball.tartarus.org/algorithms/porter/stemmer.html
2. 算法实现
Stem算法在sphinx中也是一种转型算法。 在morphology选项中可使用的内建值包括“none”,“stem_en”,“stem_ru”,“stem_enru”, “soundex”和“metaphone"。 缺省是None不使用转型算法。入口代码是在sphinx.cpp文件中的void CSphDictCRC::ApplyStemmers ( BYTE * pWord )函数里面。
void CSphDictCRC::ApplyStemmers ( BYTE * pWord )
{
// try wordforms,这个是对应配置文件中的wordforms选项,对一些用户设定的转化规则进行转化
if ( ToNormalForm ( pWord ) )
return;
// check length, 如果词语太短,小于stemm length,不使用stemm转化。
if ( m_tSettings.m_iMinStemmingLen>1 )
if ( sphUTF8Len ( (const char*)pWord )<m_tSettings.m_iMinStemmingLen )
return;
// try stemmers,在这里面进行真正的stemm转化
ARRAY_FOREACH ( i, m_dMorph )
if ( StemById ( pWord, m_dMorph [i] ) )
break;
}
七. 内存外排序算法
1. 算法原理
外部排序基本上由两个相互独立的阶段组成。首先,按可用内存大小,将外存上含n个记
录的文件分成若干长度为k的子文件或段(segment),依次读入内存并利用有效的内部排
序方法对它们进行排序,并将排序后得到的有序子文件重新写入外存。通常称这些有序
子文件为归并段或顺串;然后,对这些归并段进行逐趟归并,使归并段(有序子文件)逐
渐由小到大,直至得到整个有序文件为止。
2.代码实现
在sphinx.cpp文件中的函数int CSphIndex_VLN::Build ( )中,建立索引的过程需要进行两次分析排序。第一次分析的时候,会将读取的原始数据拆分成一个个一个数据桶(bin),数据桶内部是排序好的;第二次分析的时候,采用的是内存外排序。摘录代码如下。
//////////////
// final sort
//////////////
// 排序的算法:
// 每个bin内部事先排序,将每个bin的最小值抽取出来,作为一个最小值队列,
// 从最小值队列中中取最小值,就是全局最小值
// 将全局最小值排入新文件,并从这个全局最小值所在的bin中,取出剩余的最小值放入最小值队列中,
// 重新从最小值队列中循环上述过程。
if ( iRawBlocks )
{
int iLastBin = dBins.GetLength () - 1;
SphOffset_t iHitFileSize = dBins[iLastBin]->m_iFilePos + dBins [iLastBin]->m_iFileLeft;
CSphHitQueue tQueue ( iRawBlocks );
CSphWordHit tHit;
m_tLastHit.m_iDocID = 0;
m_tLastHit.m_iWordID = 0;
m_tLastHit.m_iWordPos = 0;
// initial fill
int iRowitems = ( m_tSettings.m_eDocinfo==SPH_DOCINFO_INLINE ) ? m_tSchema.GetRowSize() : 0;
CSphAutoArray<CSphRowitem> dInlineAttrs ( iRawBlocks*iRowitems );
int * bActive = new int [ iRawBlocks ];
for ( int i=0; i<iRawBlocks; i++ )
{
if ( !dBins[i]->ReadHit ( &tHit, iRowitems, dInlineAttrs+i*iRowitems ) )
{
m_sLastError.SetSprintf ( "sort_hits: warmup failed (io error?)" );
return 0;
}
bActive[i] = ( tHit.m_iWordID!=0 );
if ( bActive[i] )
tQueue.Push ( tHit, i );
}
// init progress meter
m_tProgress.m_ePhase = CSphIndexProgress::PHASE_SORT;
m_tProgress.m_iHits = 0;
// while the queue has data for us
// FIXME! analyze binsRead return code
int iHitsSorted = 0;
iMinBlock = -1;
while ( tQueue.m_iUsed )
{
int iBin = tQueue.m_pData->m_iBin;
// pack and emit queue root
tQueue.m_pData->m_iDocID -= m_tMin.m_iDocID;
if ( m_bInplaceSettings )
{
if ( iMinBlock == -1 || dBins[iMinBlock]->IsEOF () || !bActive [iMinBlock] )
{
iMinBlock = -1;
ARRAY_FOREACH ( i, dBins )
if ( !dBins [i]->IsEOF () && bActive[i] && ( iMinBlock == -1 || dBins [i]->m_iFilePos < dBins [iMinBlock]->m_iFilePos ) )
iMinBlock = i;
}
int iToWriteMax = 3*sizeof(DWORD);
if ( iMinBlock != -1 && m_wrHitlist.GetPos () + iToWriteMax > dBins [iMinBlock]->m_iFilePos )
{
if ( !RelocateBlock ( fdHits.GetFD (), (BYTE*)pRelocationBuffer, iRelocationSize, &iHitFileSize, dBins[iMinBlock], &iSharedOffset ) )
return 0;
iMinBlock = (iMinBlock+1) % dBins.GetLength ();
}
}
// 写对应的spi和spd文件
cidxHit ( tQueue.m_pData, iRowitems ? dInlineAttrs+iBin*iRowitems : NULL );
if ( m_wrWordlist.IsError() || m_wrDoclist.IsError() || m_wrHitlist.IsError() )
return 0;
// pop queue root and push next hit from popped bin
tQueue.Pop ();
if ( bActive[iBin] )
{
dBins[iBin]->ReadHit ( &tHit, iRowitems, dInlineAttrs+iBin*iRowitems );
bActive[iBin] = ( tHit.m_iWordID!=0 );
if ( bActive[iBin] )
tQueue.Push ( tHit, iBin );
}
// progress
if ( m_pProgress && ++iHitsSorted==1000000 )
{
m_tProgress.m_iHits += iHitsSorted;
m_pProgress ( &m_tProgress, false );
iHitsSorted = 0;
}
}
if ( m_pProgress )
{
m_tProgress.m_iHits += iHitsSorted;
m_pProgress ( &m_tProgress, true );
}
// cleanup
SafeDeleteArray ( bActive );
ARRAY_FOREACH ( i, dBins )
SafeDelete ( dBins[i] );
dBins.Reset ();
CSphWordHit tFlush;
tFlush.m_iDocID = 0;
tFlush.m_iWordID = 0;
tFlush.m_iWordPos = 0;
cidxHit ( &tFlush, NULL );
if ( m_bInplaceSettings )
{
m_wrHitlist.CloseFile ();
sphTruncate ( fdHits.GetFD () );
}
}
八.Trie tree算法
1. 算法原理
Trie树就是字典树,其核心思想就是空间换时间。
举个简单的例子。
给你100000个长度不超过10的单词。对于每一个单词,我们要判断他出没出现过,如果出现了,第一次出现第几个位置。
这题当然可以用hash来,但是我要介绍的是trie树。在某些方面它的用途更大。比如说对于某一个单词,我要询问它的前缀是否出现过。这样hash就不好弄了,而用trie还是很简单。
现在回到例子中,假设我要查询的单词是abcd,那么在他前面的单词中,以b,c,d,f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的,在以a开头中的单词中,我们只要考虑以b作为第二个字母的……这样一个树的模型就渐渐清晰了……
假设有b,abc,abd,bcd,abcd,efg,hii这6个单词,我们构建的树就是这样的。
对于每一个节点,从根遍历到他的过程就是一个单词,如果这个节点被标记为红色,就表示这个单词存在,否则不存在。如果存在,则读取附在该结点上的信息,即完成查找。
其他操作类似处理。
那么,对于一个单词,我只要顺着他从跟走到对应的节点,再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色,就相当于插入了这个单词。 这样一来我们询问和插入可以一起完成。
我们可以看到,trie树每一层的节点数是26^i级别的(i表示层数)。所以为了节省空间。我们用动态链表,或者用数组来模拟动态。空间的花费,不会超过单词数×单词长度。
Trie树的缺点是内存耗费大,尤其对于中文,因为中文字数多,词汇排列多,导致内存耗费非常大。一般会使用double array trie的方式来实现,以便减少内存耗费。
2. 算法实现
在sphinx中是使用double array 来实现trie算法,这一部分的算法实现请参考下面一节的double array trie的算法中的实现。算法的使用可以参考unigramdict.cpp中的函数int UnigramDict::findHits()。
九. Double-Array trie算法
1. 算法原理
Double Array Trie是TRIE树的一种变形,它是在保证TRIE树检索速度的前提下,提高空间利用率而提出的一种数据结构,本质上是一个确定有限自动机(deterministic finite automaton,简称DFA)。
对于Double Array Trie(以下简称DAT),每个节点代表自动机的一个状态,根据变量的不同,进行状态转移,当到达结束状态或者无法转移的时候,完成查询。
DAT是采用两个线性数组(base[]和check[]),base和check数组拥有一致的下标,(下标)即DFA中的每一个状态,也即TRIE树中所说的节点,base数组用于确定状态的转移,check数组用于检验转移的正确性。因此,从状态s输入c到状态t的一个转移必须满足如下条件:
(1) base[s] + c == t
(2) check[base[s] + c] == s
DAT也可如下描述:
l 对于给定的状态s,如果有n个状态(字符c1,c2,...,cn)的转移,需要在base数组中找到一段空位t1,t2,...,tn,使得t1-c1,t2-c2,...,tn-cn都为base数组中下标为s的值,注意此处的t1,t2,...,tn不一定在base数组中连续;
l 对于转移的状态t1,t2,...,tn,其作为下标时,check[t1],check[t2],...,check[tn]的值都为状态s;
DAT匹配
基于上述定义,DAT的匹配过程如下:假设当前状态为s,对于输入的字符c有:
t = base[s] + c;
if check[t] = s then
next state = t;
else
fail;
endif
DAT匹配的过程相对简单,很容易理解。
算法的复杂性在于构造满足DAT两个条件的数组。有多种构造方式,因为程序中使用的是darts的第三方组件来实现double array算法,因此我们并不需要太关心其实现,而更多关注其应用,因此这里不详细讲解其算法原理。具体可以参考相关的算法介绍书籍。推荐一个讲解比较详细的链接:http://linux.thai.net/~thep/datrie/datrie.html
2. Darts的应用接口
程序中并没有直接实现double_array算法,而是利用第三方开源组件darts实现的double-array算法。 这里只把darts的使用方法进行简单介绍,并例举了sphinx程序中的应用程序进行讲解,但并没有对darts的实现进行说明。如果有兴趣,可以研究darts的实现。
Darts 是用于构建双数组 Double-Array 的简单的 C++ Template Library . 双数组 (Double-Array) 是用于实现 Trie 的一种数据结构, 比其它的类 Trie 实现方式(Hash-Tree, Digital Trie, Patricia Tree, Suffix Array) 速度更快。 原始的 Double-Array 使能够支持动态添加删除 key, 但是 Darts 只支持把排好序的词典文件转换为静态的 Double-Array.
使用方法
Darts 只提供了 darts.h 这个 C++ 模板文件。每次使用的时候 include 该文件即可.
使用这样的发布方式是希望通过内联函数实现高效率。
类接口
namespace Darts {
template <class NodeType, class NodeUType class ArrayType,
class ArrayUType, class LengthFunc = Length<NodeType> >
class DobuleArrayImpl
{
public:
typedef ArrayType result_type;
typedef NodeType key_type;
DoubleArrayImpl();
~DoubleArrayImpl();
int set_array(void *ptr, size_t = 0);
void *array();
void clear();
size_t size ();
size_t unit_size ();
size_t nonzero_size ();
size_t total_size ();
int build (size_t key_size,
key_type **key,
size_t *len = 0,
result_type *val = 0,
int (*pg)(size_t, size_t) = 0);
int open (const char *file,
const char *mode = "rb",
size_t offset = 0,
size_t _size = 0);
int save (const char *file,
const char *mode = "wb",
size_t offset = 0);
result_type exactMatchSearch (const key_type *key,
size_t len = 0,
size_t node_pos = 0)
size_t commonPrefixSearch (const key_type *key,
result_type *result,
size_t result_size,
size_t len = 0,
size_t node_pos = 0)
result_type traverse (const key_type *key,
size_t &node_pos,
size_t &key_pos,
size_t len = 0)
};
typedef Darts::DoubleArrayImpl<char, unsigned char,
int, unsigned int> DoubleArray;
};
模板参数说明
| NodeType |
Trie 节点类型, 对普通的 C 字符串检索, 设置为 char 型即可. |
| NodeUType |
Trie 节点转为无符号整数的类型, 对普通的 C 字符串检索, 设置为 unsigned char 型即可. |
| ArrayType |
Double-Array 的 Base 元素使用的类型, 通常设置为有符号 32bit 整数 |
| ArrayUType |
Double-Array 的 Check 元素使用的类型, 通常设置为无符号 32bit 整数 |
| LengthFunc |
使用 NodeType 数组的时候,使用该函数对象获取数组的大小, 在该函数对象中对 operator() 进行重载. |
typedef 说明
模板参数类型的别名. 在外部需要使用这些类型的时候使用 .
| key_type |
待检索的 key 的单个元素的类型. 等同于 NodeType. |
| result_type |
单个结果的类型. 等同于 ArrayType . |
方法说明
(1) int Darts::DoubleArrayImpl::build(size_t size, const key_type **str, const size_t *len = 0, const result_type *val = 0, int (*progress_func)(size_t, size_t) = 0)
构建 Double Array .
size 词典大小 (记录的词条数目),
str 指向各词条的指针 (共 size个指针)
len 用于记录各个词条的长度的数组(数组大小为 size)
val 用于保存各词条对应的 value 的数组 (数组大小为 size)
progress_func 构建进度函数.
str 的各个元素必须按照字典序排好序.
另外 val 数组中的元素不能有负值.
len, val, progress_func 可以省略,
省略的时候, len 使用 LengthFunc 计算,
val 的各元素的值为从 0 开始的计数值。
构建成功,返回 0; 失败的时候返回值为负.
进度函数 progress_func 有两个参数.
第一个 size_t 型参数表示目前已经构建的词条数
第二个 size_t 型参数表示所有的词条数
(2) result_type Darts::DoubleArrayImpl::exactMatchSearch(const key_type *key, size_t len = 0, size_t node_pos = 0)
进行精确匹配(exact match) 检索, 判断给定字符串是否为词典中的词条.
key 待检索字符串,
len 字符串长度,
node_pos 指定从 Double-Array 的哪个节点位置开始检索.
len, 和 node_pos 都可以省略, 省略的时候, len 缺省使用 LengthFunc 计算,
node_pos 缺省为 root 节点.
检索成功时, 返回 key 对应的 value 值, 失败则返回 -1.
(3) size_t Darts::DoubleArrayImpl::commonPrefixSearch (const key_type *key, result_type *result, size_t result_size, size_t len = 0, size_t node_pos = 0)
执行 common prefix search. 检索给定字符串的哪些的前缀是词典中的词条
key 待检索字符串,
result 用于保存多个命中结果的数组,
result_size 数组 result 大小,
len 待检索字符串长度,
node_pos 指定从 Double-Array 的哪个节点位置开始检索.
len, 和 node_pos 都可以省略, 省略的时候, len 缺省使用 LengthFunc 计算,
node_pos 缺省为 root 节点.
函数返回命中的词条个数. 对于每个命中的词条, 词条对应的 value 值存依次放在 result 数组中. 如果命中的词条个数超过 result_size 的大小, 则 result 数组中只保存 result_size 个结果。函数的返回值为实际的命中词条个数, 可能超过 result_size 的大小。
(4)result_t Darts::DoubleArrayImpl::traverse (const key_type *key, size_t &node_pos, size_t &key_pos, size_t len = 0)
traverse Trie, 检索当前字符串并记录检索后到达的位置
key 待检索字符串,
node_pos 指定从 Double-Array 的哪个节点位置开始检索.
key_pos 从待检索字符串的哪个位置开始检索
len 待检索字符串长度,
该函数和 exactMatchSearch 很相似. traverse 过程是按照检索串 key 在 TRIE 的节点中进行转移.
但是函数执行后, 可以获取到最后到达的 Trie 节点位置,最后到达的字符串位置 . 这和 exactMatchSearch 是有区别的.
node_pos 通常指定为 root 位置 (0) . 函数调用后, node_pos 的值记录最后到达的 DoubleArray 节点位置。
key_pos 通常指定为 0. 函数调用后, key_pos 保存最后到达的字符串 key 中的位置。
检索失败的时候, 返回 -1 或者 -2 .
-1 表示再叶子节点失败, -2 表示在中间节点失败,.
检索成功的时候, 返回 key 对应的 value.
(5)int Darts::DoubleArrayImpl::save(const char *file, const char *mode = "wb", size_t offset = 0)
把 Double-Array 保存为文件.
file 保存文件名,
mode 文件打开模式
offset 保存的文件位置偏移量, 预留将来使用, 目前没有实现 .
成功返回 0 , 失败返回 -1
(6)int Darts::DoubleArrayImpl::open (const char *file, const char *mode = "rb", size_t offset = 0, size_t size = 0)
读入 Double-Array 文件.
file 读取文件名,
mode 文件打开模式
offset 读取的文件位置偏移量
size 为 0 的时候, size 使用文件的大小 .
成功返回 0 , 失败返回 -1
(7)size_t Darts::DoubleArrayImpl::size()
返回 Double-Array 大小.
size_t Darts::DoubleArrayImpl::unit_size()
Double-Array 一个元素的大小(byte).
size() * unit_size() 是, 存放 Double-Array 所需要的内存(byte) 大小.
size_t Darts::DoubleArrayImpl::nonzero_size()
Double-Array 的所有元素中, 被使用的元素的数目, .
nonezero_size()/size() 用于计算压缩率.
3. 程序应用代码
Sphinx的darts接口api在darts.h中定义。有多个地方应用了double array的数组结构来构造字典。包括unigramdict.cpp, thesaurusdict.cpp, synonymsdict.cpp。分别用来构造分词词典,同义词/复合分词词典和特殊短语转化的词典。
代码都是调用darts的接口,比较简单,只要知道darts的接口作用就比较简单了。
转自http://blog.csdn.net/uestc_huan/article/details/6395160