(HDU1061||nefu783)&&nefu 66 求N^N的最右边和最左边的数
http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=783
http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=66
先说简单一点的:要求该数的最右边的一个数字我们可以发现它只和n的个位数有关,而且有一点的循环性,循环节肯定小于10,因此我们可以利用找循环节的方法来想。
#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;
typedef long long LL;
LL n;
int num[100];
bool flag[100];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int a=n%10;
if(a==0)
{
printf("0\n");
continue;
}
int b=a;
memset(num,0,sizeof(num));
memset(flag,false,sizeof(flag));
int i=0;
while(!flag[a])
{
num[i++]=a;
flag[a]=true;
a=(b*a)%10;
}
int sum=i;
/*for(int i=0;i<sum;i++)
printf("%d ",num[i]);
printf("\n");*/
printf("%d\n",num[(n-1)%sum]);
}
return 0;
}
对于求其最左边的数就需要考虑一下了:N^N=d.xxxxxxx*10^(k-1),k表示N^N的位数:k=(int)log10(N^N)+1,d即为所求。我们可以推出公式:
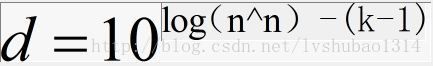
#include <stdio.h>
#include <string.h>
#include <math.h>
using namespace std;
typedef long long LL;
double a;
LL n;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%lld",&n);
a=n*log10(n);
a-=(LL)a;
printf("%lld\n",(LL)pow(10,a));
}
return 0;
}