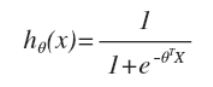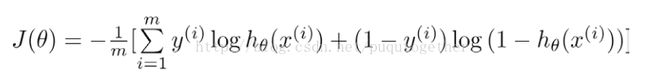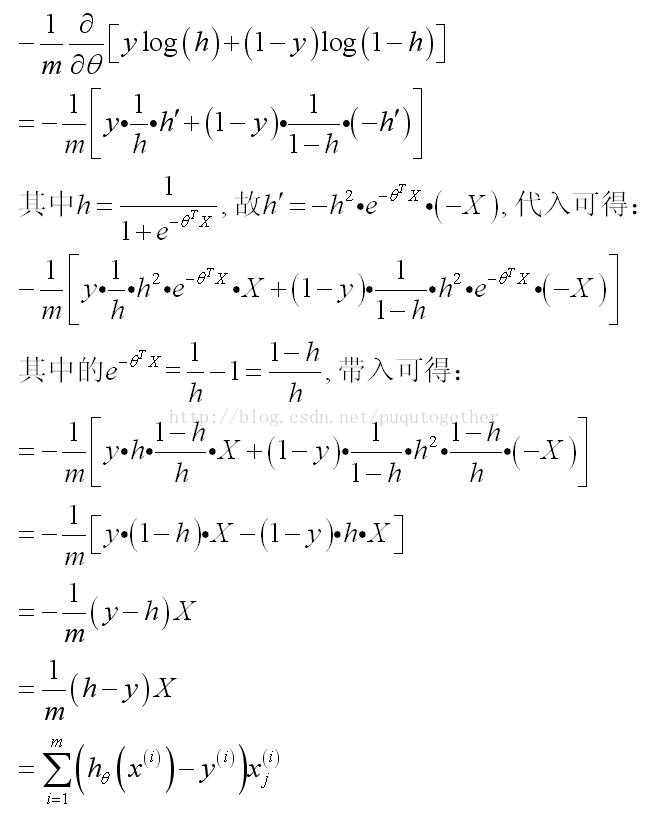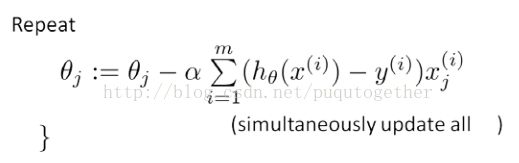Stanford机器学习课程笔记——LR的公式推导和过拟合问题解决方案

Stanford机器学习课程笔记——LR的公式推导和过拟合问题解决方案

    

1. Logistic Regression

    前面说的单变量线性回归模型和多变量线性回归模型，它们都是线性的回归模型。实际上，很多应用情况下，数据的模型不是一个简单的线性表示就可以搞定的（后面的稀疏表示和字典学习又再次回到的线性表示，当然这个是后话）。更多的时候，我们需要建立一个非线性的模型。此时，Logistic Regression就诞生了。

    LR的假设模型：

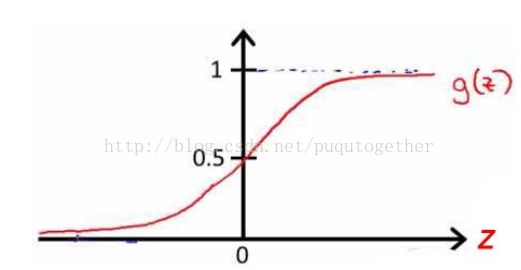
    前面的线性模型都是线性方程作为假设模型，这里的LR使用的逻辑函数，又称为S型函数。

为什么使用这个逻辑函数呢？其实后面有着既内涵有巧妙地原因：

• 这个函数对于给定的输入变量，会根据选择的参数计算输出变量=1的可能性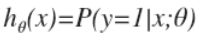，，也就是说它的输出表示概率，都是0到1之间；
• 该S型假设模型函数融入到后面的代价函数中之后，在梯度下降法中求导之后的模型，巧妙地和前面线性模型的求导形式一致。

    LR的代价函数：

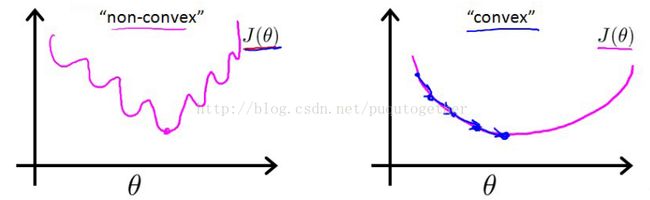
    有了前面的假设，我们当然可以使用之前熟悉的误差平方和来作为代价函数。但是，我们会发现这时候的代价函数是非凸的，也就是函数图像中会出现许多的局部最小值，导致梯度下降法极其容易得到局部最小值。如下：

所以，我们需要重新设置代价函数形式。LR中的代价函数如下：

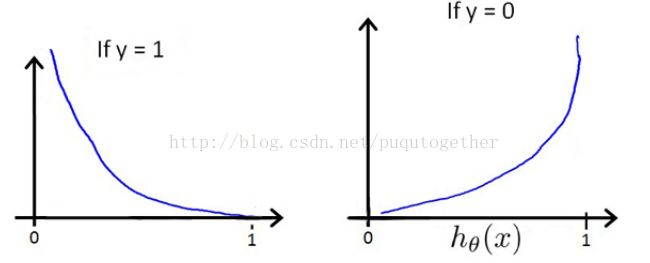
选择这样子的代价函数的原因如下：

• 当实际的y=1和预测的h_theta也为1的时候，误差=0，误差会随着h_theta的变小而增大；当y=0和h_theta=0的时候，误差=0,误差会随着h_theta的增大而增大；
• 代价函数的求导形式和线性模型的求导形式巧妙的相似。（这部分有两个原因，前面已经提到一个了）

2. LR的梯度下降法公式推导

    给定上面定义的假设和代价函数，而且此时的代价函数也是非凸的，我们便可以使用梯度下降法求出令代价函数最小时的theta向量。梯度下降法的基本算法如下：

此时关键的时候要把J_theta对theta的导数求出来。具体的公式推导比较复杂，如下：

（其中的假设我直接用h简单表示）

然后，LR的梯度下降算法就成为了：

发现这个形式和前面线性回归模型的梯度下降法巧妙的一致了。

当然，后面我们就可以使用这个算法来求解LR模型了。

3. 解决过拟合问题

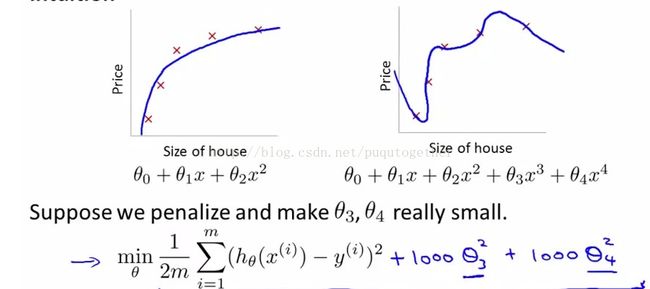
    什么是过拟合问题？就是我们训练出来的模型可以很好的适应所有的训练样本，但是不能对测试样本很好地预测，这就是过拟合问题。如下图所示：

解决过拟合的方法有两个：

（1） 降维，可以使用PCA算法把样本的维数降低，使得模型的theta的个数减少，次数也会降低，避免了过拟合；

（2） 正则化，设计正则项regularization term, 也可以避免过拟合。这种方法下面详细说一下。

正则化的方式有几种：

1. 可以给一些参数项加惩罚；

     比如下面的模型：

由于高次项的theta_3和theta_4比较大，所以我们需要对这两项乘以惩罚，也就是在代价函数的后面对这两个theta_3和theta_4加一个很大的权重。

    那么当我们不知道哪几项需要惩罚的时候，我们就会在代价函数中给每一项的theta都加一个惩罚，称为给代价函数加一个正则项。如下：

同样地，对于LR回归，我们也可以在它的代价函数后面添加一个正则项，这样子我们也可以避免过拟合。

    其实，每次更新theta的时候，都会额外减去一个(lambda/m)*theta_j。这样会使得求解出来的theta普遍小一下。但是，我们要注意正则项前面的因子lambda的设置，如果lambda设置过大，会导致求解出来的所有theta都很小，甚至等于0 。