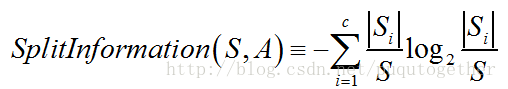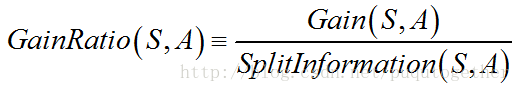初窥决策树中的ID3和C4.5

初窥决策树中的ID3和C4.5

虽说教研室做的都是machine learning and data mining的方法，但是几乎还是围绕着dictionary learning, multi-view learning, metric learning等等这些techniques，而对一些经典的机器学习算法了解的还不好、昨天花了一个下午看了一下decision tree部分，所以有了这篇学习笔记。

决策树的基本概念

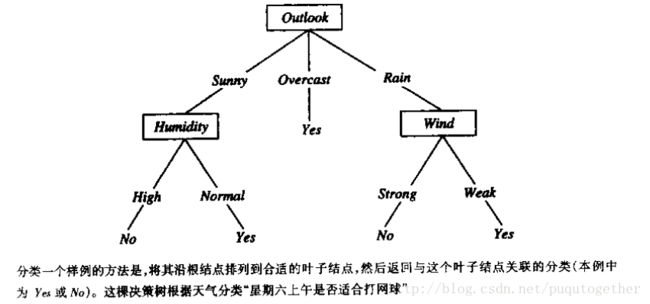
决策树把实例从根结点排列到下面许多层的叶子结点，进而实现分类。其中没有叶子结点（包括根结点），都是每个实例所属的分类。在决策树中，每一个结点都会对实例的某个属性进行依次判断，判断出该结点的每个后继分支对应于该属性的一个可能值。当构建好决策树之后，我们就可以对测试实例进行分类。我们可以按照给定实例在每个结点（包括根结点）的属性值，判断应该沿着结点后的哪一条分支向下移动。一直向下移动判断，最终得到对测试实例的分类。如下图所示：

如果按照经典机器学习中合取/析取的概念来描述，那么决策树代表实例属性值约束的合取（conjunction）和析取式（disjunction）。从根结点到树叶的每一条路径对应一组属性测试的合取，决策树本身对应这些合取的析取。

ID3

这是一个采用自顶向下的贪婪搜索遍历可能的决策空间算法。

基本的ID3算法通过自顶向下来构造决策树，进行学习。

首先，需要挑选出一个属性，作为决策树的根结点。挑选的规则就是将分类能力最好的属性作为根结点。我们可以使用统计测试来确定每一个实例属性单独分类训练测试样本的能力。

然后，根结点属性的每一个可能值都会产生一个分支，我们需要把所有的训练样本排列到适当的分支之下。

然后，在每个分支下再选择出一个叶子的结点，这里挑选的规则和跳出根结点的规则一致；

重复上述过程，用每个分支结点关联的训练样本来选取在该点被测试的最佳属性，直到我们可以把每一个训练样本分类为止。

从上面ID3的算法步骤可以看出：该算法形成了对合格决策树的贪婪搜索（greedy search），该算法没有回溯的过程。换句话说，当选择好了根结点或者是叶子的结点之后，它就不会再回头考虑之前的选择，这一点和之前总结的回溯算法有很大的不同。

我们很容易发现，在ID3的算法步骤中，关键的是那个挑选规则，无论对于根结点还是叶子结点而言。因为有了挑选规则，所以我们才可以判断出哪个属性才是最佳的分类属性。那么在ID3中，我们使用信息增益（information gain）来衡量每一个属性区分训练样本的能力。下面我们将详细介绍如何计算一个属性的信息增益。

信息增益的定义是基于信息论中的熵（entrophy），它刻画了任意样本集的纯度。给定一个样本集，那么我们可以根据其中正样本和反样本的比例来计算出样本集S的熵，计算公式如下：

其中是样本集中正样本所占的比例，是负样本所占的比例。0log0=0.

那么，一个属性A相对于样本集S的信息增益Gain(S,A)就有如下定义：

其中，Values(A)是属性A所有可能值的集合。上式中，第一项就是原集合S的熵，第二项是用A分类S后的熵的期望值，也就是每个子集的熵的加权和。所以Gain(S,A)就是知道属性A的值而导致的期望熵的减少，是由于个顶属性A的值而得到的关于目标函数值的信息，也是在知道属性A的值后可以节省的二进制位数。

以上定义的信息增益information gain就是ID3算法使用到的在每一步中选取最佳属性的度量标准。我们可以计算每一个属性对应的gain值，然后选择其中最大增益对应的属性来作为根结点或是叶子结点。需要注意的是，对于非终端的后继结点，我们在重复计算新属性的gain值的时候，用到的训练样本仅仅是和该结点关联的训练样本。已经被前面较高结点测试过的属性需要排除在外。也就是说，所有属性在决策树上任意的路径出现的次数只能是一次。

算法步骤中终止的条件有两个：

1）所有的属性已经被路径包括了；

2）这个结点关联的所有训练样本都具有相同的目标属性值（即熵为0）。

ID3算法的优缺点

1）ID3算法中的假设空间包含了所有的决策树，它是关于现有属性的有限离散值函数的一个完整空间。所以该算法避免了假设空间可能不包含目标函数的风险；

2）当遍历决策树空间时，ID3仅仅考虑了单一的当前假设，故该算法失去了表示所有一致假设所带来的优势，即不能找出所有符合条件的决策树；

3）基本的ID3算法在搜索中不进行回溯。在无回溯的爬山搜索中，最常见的分线就是：收敛到局部最优的答案，而不是全局最优。这里我们可以增加回溯，如修剪决策树（C4.5）；

4）ID3算法在搜索的每一步都使用当前的所有训练样本，以统计为基础决定怎样精化当前的假设。因为使用到了所有样本的统计信息，所以对训练样本中的噪声不敏感，具有较好的健壮性。

ID3归纳偏置：较短的树比较长的树优先，信息增益高的属性更靠近根结点的树优先。

决策树中常见的问题

决策树学习过程中会经常遇到如下问题：确定决策树增长的深度；处理连续值的属性；选择一个适当的属性筛选度量标准；处理属性值不完整的训练样本；处理不同代价的属性；提高计算效率等等。那么C4.5就是在解决了如上这些问题之后得到的一种改进决策树算法。

1）避免过度拟合数据

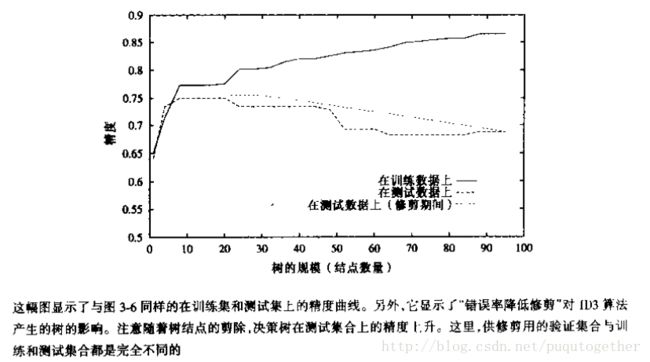
理想的决策树学习算法中，我们可以恰好的对训练样本完美的分类。但是，当数据中含有噪声，或者是训练样本的个数太少的时候，就会出现过度拟合的现象。换句话说，过度拟合想象就是存在另外一种假设，其在某个树的规模（深度）的时候错误率（分类效果）比最终求的假设大，但是整体来看，这样的另外一种假设错误率最小。这就是过度拟合。

两种方法解决过度拟合：

a、及早停止树的增长，在ID3算法完美分类训练数据之前就可以停止增长；

b、后修剪法，即允许树过度拟合数据，然后在得到的决策树上进行后续的修剪。

规则后修剪法：

Step 1：从训练样本集中推导出决策树，增长决策树直到尽可能好地拟合训练样本，这里允许过度拟合的发生；

Step 2：将决策树转化为等价的规则集合，方法是为从根结点到叶子及诶但的每一条路径创建一条规则；

Step 3：通过删除任何能导致估计精度的前件来修剪）泛化 每一条规则；

step 4：按照修剪过的规则的估计精度对它们进行排序，并按照这样的顺序应用这些规则来分类后来的实例。

2）合并连续值属性

对于连续值属性，我们只需要把连续值属性采样称为离散的区间就可以了，之后构建决策树的步骤和前面一样。

3）属性选择的其他度量标准

信息增益度量标准的一个缺陷就是：偏袒了具有较多值的属性。避免这个不足的一种方法就是用增益比率（gain ratio）作为度量标准，这也是C4.5算法中用来选择属性的度量标准。

相对于信息增益，增益比率增加了一个分裂信息（split information），它是用来惩罚具有较多值的属性的。分裂信息用来衡量属性分裂数据的广度和均匀性，其计算公式如下：

我们可以看出，分裂信息其实就是S关于属性A的各值的熵。

那么增益比率就是：

使用增益比率得到的选择属性的效果显然更好。

4）处理缺少属性值的训练样本

树立缺少属性值的一种策略就是赋给它结点n的训练样本中该属性的最常见的值。或者是赋给它结点n的被分类为c(x)的训练样本中该属性的最常见的值。

5）处理不同代价的属性

引入代价敏感项（cost-sensitive term），这个是教研室中经常用到的technique。