分治+贪心

《算法竞赛入门经典》---高效算法设计，作者的编辑思路，是首先介绍了算法的效率分析。 其中规模与运算量的对应关系大致为：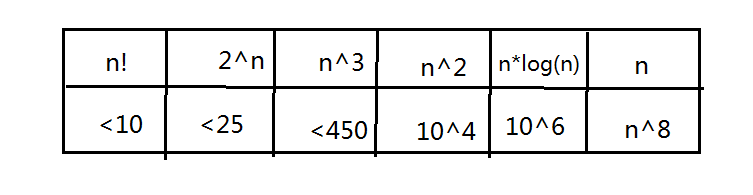
然后谈到归并排序、快速排序和二分查找，推荐对 [ )的使用，然后谈到二分查找中的集中具体情况bsearch,lower_bound（找上界（即：第一个元素下标））,upper_bound（找下界（最后一个元素的下一个下标）），

然后介绍分治法，分治法三步走：

划分问题：把问题分成子问题

递归求解：递归求解子问题

合并问题：合并子问题的解

另外一些心得：分治法的效率主要体现在合并子问题的算法中，仔细分析下面中的第二题

最后谈到贪心法，使用贪心法要满足的两个条件：

①贪心选择

②最优子结构

本章需要掌握：

①前n个数之和sum[n]的使用

②前开后闭区间，[ )的使用

下面一些是推荐题型：

分治法的应用：

一、最大字段和

二、逆序对数（推荐）

三、归并排序（基础）

四、快速排序（基础）

五、二分查找（基础，基础）

六、棋盘覆盖

七、循环日程表

八、非线性求根

九、最大值最小化（推荐）

贪心法的应用：

十、选择不相交区间（推荐）

十一、Huffman编码

一、最大字段和

//解法一：分治法实现

#include <cstdio>
const int nMax = 100;
int fmax(int a, int b)
{
	return a>b?a:b;
}
int bsearch(int *A,int l,int r)
{
	if(1 == r - l) return A[l];
	int mid=l+(r-l)/2;
	int max1=bsearch(A,l,mid);
	int max2=bsearch(A,mid,r);
	int sum,max3,max4;
	int i;
	for(i = mid-1, sum = 0, max3 = A[i]; i >= l; -- i)
	{
		sum += A[i];
		if(sum > max3)
			max3 = sum;
	}
	for(i = mid, sum = 0, max4 = A[i]; i < r; ++ i)
	{
		sum += A[i];
		if(sum > max4)
			max4 = sum;
	}
	return fmax(fmax(max1, max2), max3 + max4);
}
int main()
{
	int A[nMax];
	int i;
	int N;
	scanf("%d", &N);
	for(i = 1; i <= N; ++ i)
		scanf("%d", &A[i]);
	printf("%d",bsearch(A,1,N+1));
	return 0;
}

//解法二：sum[]，设（a，b）为最大区间，如果b确定，则只需要找到b之前sum[i]的最小值即可，这样(a,b)就会最大
#include <cstdio>
const int nMax = 100;
int main()
{
	int A[nMax];
	int N;
	int i;
	int sum[nMax];
	sum[0] = 0;
	scanf("%d", &N);
	for(i = 1; i <= N; ++ i)
		sum[i] = sum[i-1] + A[i];
	int res=A[1],
		min=0;
	for(i = 1; i <= N; ++ i)
	{
		if(sum[i] - min > res)
			res = sum[i] - min;
		if(sum[i] < min)
			min = sum[i];
	}
	printf("%d\n",res);
	return 0;
}

二、逆序对数

/*
在进行合并子问题时，如果仍然是按照正常的思维找出i在左边，j在右边，其实算法的效率并没有得到提高，
O(T)=O(T/2)+O(n*n/4)，所以最后O(T)仍然为O(n*n)，所以分治法的效率主要体现在合并子问题的算法中。
*/
#include <cstdio>
#include <cstring>
const int nMax = 100;
int N;
int A[nMax];
void init()
{
	scanf("%d", &N);
	int i;
	for(i = 1; i <= N; i++)
		scanf("%d", &A[i]);
}
int MergeSort_search(int l, int r)
{
	if(1 == r - l) return 0;
	int mid = l + (r - l) / 2;
	int sum = 0;
	sum += MergeSort_search(l, mid);
	sum += MergeSort_search(mid, r);
	int i,j;
	int B[nMax];
	int len=l;
	for(i = l, j = mid;i < mid || j < r; )
	{
		if(i == mid) B[len ++] = A[j ++];
		else if(j == r) B[len ++] = A[i ++];
		else 
		{
			if(A[i] <= A[j])
				B[len ++] = A[i ++];
			else
			{
				B[len ++] = A[j ++];
				sum += mid - i;
			}
		}
	}
	memcpy(A+l,B+l,(len - l) * sizeof(int));
	return sum;
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	int ans = MergeSort_search(1,N+1);
	printf("%d\n",ans);
	return 0;
}

三、归并算法

#include <cstdio>
#include <cstring>
const int nMax = 100;
int N;
int A[nMax];
void init()
{
	scanf("%d", &N);
	int i;
	for(i = 1; i <= N; i++)
		scanf("%d", &A[i]);
}
void MergeSort(int l, int r)
{
	if(1 == r - l) return;
	int mid = l + (r - l) / 2;
	MergeSort(l, mid);
	MergeSort(mid, r);
	int i,j;
	int B[nMax];
	int len=l;
	for(i = l, j = mid;i < mid || j < r; )
	{
		if(i == mid) B[len ++] = A[j ++];
		else if(j == r) B[len ++] = A[i ++];
		else 
		{
			if(A[i] < A[j])
				B[len ++] = A[i ++];
			else 
				B[len ++] = A[j ++];
		}
	}
	memcpy(A+l,B+l,(len - l) * sizeof(int));
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	MergeSort(1,N+1);
	int i;
	for(i = 1; i <= N; ++ i)
		printf("%d ", A[i]);
	printf("\n");
	return 0;
}

四、快速排序

//#define TEST
#include <cstdio>
#include <cstring>
const int nMax = 100;
int N;
int A[nMax];
void init()
{
	scanf("%d", &N);
	int i;
	for(i = 1; i <= N; i++)
		scanf("%d", &A[i]);
}
void print()
{
	int i;
	for(i = 1; i <= N; i++)
		printf("%d ", A[i]);
	printf("\n");
}
int partition(int l, int r)
{
	int temp = A[l];
	int left = l,
		right = r - 1;
	while(left < right)
	{
		while(left < right && A[right] >= temp) -- right;//这里曾经出了点小错，是>=，不能只是单单只有>
		if(left < right) A[left] = A[right];
		while(left < right && A[left] <= temp) ++ left;
		if(left < right) A[right] = A[left];
	}
	A[left] = temp;
	return left;
}
void quickSort(int l, int r)
{
#ifdef TEST
	printf("%d %d \n",l,r);
#endif
	if(1 >= r - l) return;
	int p = partition(l, r);
	quickSort(l, p);
	quickSort(p+1, r);
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	quickSort(1,N+1);
	print();
	return 0;
}

五、二分查找

/*
二分查找的三种形式，可以使用upper_search和lower_search查找一个区间内某个整数的个数，
仔细体会①处的原因，最后一个查找的元素一定是落在left上这是因为求mid向下取整的原因，使得left不会跳过任何一个元素。
还有需要注意②处的处理，这是做题的技巧，这样可保证最终结果定为left，细节处理要仔细。这个从lower_search()这里来领悟会更容易一些。
*/
#include <cstdio>
#include <cstring>
const int nMax = 100;
int N;
int A[nMax];
void init()
{
	scanf("%d", &N);
	int i;
	for(i = 1; i <= N; i++)
		scanf("%d", &A[i]);
}
int bsearch(int e, int l, int r)
{
	int left = l,
		right = r - 1;//③，这里的right需要是实际值
	while(left < right)
	{
		int mid = left + (right - left) / 2;
		if(e == A[mid]) return mid;
		else if(e < A[mid]) right = mid;//②这里是right = mid，而不是right = mid - 1;
		else left = mid + 1;
	}
	//①left肯定为最后查找的元素，而right则不一定，自己体会
	if(e == A[left]) return left;
	else return -1;
}
int lower_bound(int e, int l, int r)
{
	int left = l,
		right = r - 1;
	while(left < right)
	{
		int mid = left + (right - left) / 2;
		if(e <= A[mid]) right = mid;//②这里是right = mid，而不是right = mid - 1;
		else left = mid + 1;
	}
	if(e == A[left]) return left;
	else return -1;
}
int upper_bound(int e, int l, int r)
{
	int left = l,
		right = r - 1;
	while(left < right)
	{
		int mid = left + (right - left) / 2;
		if(e < A[mid]) right = mid;
		else left = mid + 1;
	}
	if(e == A[left-1]) return left;
	else return -1;
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	int e;
	scanf("%d",&e);
	printf("%d %d %d\n",bsearch(e, 1, N + 1), lower_bound(e, 1, N + 1),upper_bound(e, 1, N + 1));
	return 0;
}

六、棋盘覆盖

#include <cstdio>
const int nMax = 100;
int A[nMax][nMax];
int t;
void cover(int x,int y,int size,int a,int b)
{
	if(1 == size) return;
	size /= 2;
	++ t;
	//左上角
	if(a < x + size && b < y + size)
	{
		A[x + size][y + size - 1]=t;
		A[x + size - 1][y + size]=t;A[x + size][y + size]=t;
		cover(x, y, size, a, b);
		cover(x + size, y, size, x + size, y + size - 1);
		cover(x, y + size, size, x + size - 1, y + size);
		cover(x + size, y + size, size, a + size, b + size);
	}
	//左下角
	else if(a < x + size && b >= y + size)
	{
		A[x + size - 1][y + size - 1]=t;A[x + size][y + size - 1]=t;
		A[x + size][y + size]=t;
		cover(x, y, size, x + size - 1, y + size - 1);
		cover(x + size, y, size, x + size, y + size - 1);
		cover(x, y + size, size, a, b);
		cover(x + size, y + size, size, a + size, b + size);
	}
	//右上角
	else if(a >= x + size && b < y + size)
	{
		A[x + size - 1][y + size - 1]=t;
		A[x + size - 1][y + size]=t;A[x + size][y + size]=t;
		cover(x, y, size, x + size - 1, y + size - 1);
		cover(x + size, y, size, a, b);
		cover(x, y + size, size, x + size - 1, y + size);
		cover(x + size, y + size, size, a + size, b + size);
	}
	//右下角
	else if(a >= x + size && b >= y + size)
	{
		A[x + size - 1][y + size - 1]=t;A[x + size][y + size - 1]=t;
		A[x + size - 1][y + size]=t;
		cover(x, y, size, x + size - 1, y + size - 1);
		cover(x + size, y, size, x + size, y + size - 1);
		cover(x, y + size, size, x + size - 1, y + size);
		cover(x + size, y + size, size, a, b);
	}
}
int main()
{
	freopen("f://data.in","r",stdin);
	int k;
	scanf("%d", &k);
	int a,b;
	scanf("%d%d", &a, &b);
	A[a][b]=-1;
	int n = 1 << k;
	t=0;
	cover(1, 1, n, a, b);
	int i,j;
	for(i = 1; i <= n; ++ i)
	{
		for(j = 1; j <= n; ++ j)
		{
			printf("%-5d",A[i][j]);
		}
		printf("\n");
	}
	return 0;
}

七、循环日程表

#include <cstdio>
const int nMax = 100;
int A[nMax][nMax];
void arrange(int size)
{
	if(1 == size) 
	{
		A[1][1] = 1;
		return;
	}
	size /= 2;
	arrange(size);
	int i, j;
	for(i = 1; i <= size; ++ i)
		for(j = 1; j <= size; ++ j)
		{
			A[i+size][j+size] = A[i][j];
			A[i+size][j]=A[i][j]+size;
			A[i][j+size]=A[i][j]+size;
		}
}
int main()
{
	int k;
	scanf("%d",&k);
	int n = 1 << k;
	arrange(n);
	int i, j;
	for(i = 1; i <= n; ++ i)
	{
		for(j = 1; j <= n; ++ j)
			printf("%-5d",A[i][j]);
		printf("\n");
	}
	return 0;
}

九、最大值最小化

/*
题意：将n个正整数的序列划分成m个连续的序列，设第i个序列的各数之和为S(i)，你的任务是让所有的S(i)的最大值最小

解决这道题，直接从结果出发，结果的最大值为x，然后在[0,x]区间内寻找结果，找出满足情况的最小值。设结果为k，则只需要尽量向右走即可
限制条件为序列之和不能超过k
*/
#include <cstdio>
#include <cstring>
const int nMax = 100;
int N,M;
int A[nMax];
void init()
{
	scanf("%d %d", &N,&M);
	int i;
	for(i = 0; i < N; i++)
		scanf("%d", &A[i]);
}
bool f(int p)
{
	int t=1;
	int sum=0;
	int i;
	for(i = 0; i < N; ++ i)
	{
		if(sum + A[i] <= p)
		{
			sum += A[i];
		}
		else
		{
			sum = A[i];
			++ t;
		}
		if(t > M)
			return 0;
	}
	return 1;
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	int left=0,
		right=10;
	while(left < right)
	{
		int mid = left + (right - left) / 2;
		if(f(mid)) right = mid;
		else left = mid + 1;
	}
	printf("%d\n",left);
	return 0;
}

十、选择不相交区域

/*
数轴上有n个开区间(ai,bi)，选择尽量多个区间，使得这些区间两两没有公共点

思路：首先按ai的值进行一次排序，然后会出现：
情况一：b1 > b2，对于这种情况直接舍掉第一组
情况二：在情况一都被排除后，bi也成递增，这时的贪心策略是，选1不选2，然后排除与1相交的区域，
如果选2不选1，那么最右边会比较大，所以肯定不如前面一种策略好。
*/
#include <cstdio>
#include <cstdlib>
const int nMax = 100;
struct Node
{
	int a;
	int b;
}node[nMax];
int N;
int visit[nMax];
void init()
{
	scanf("%d", &N);
	int i;
	for(i = 0; i < N; ++ i)
		scanf("%d %d", &node[i].a, &node[i].b);

}
int cmp(const void *a,const void *b)
{
	Node *pa = (Node *) a;
	Node *pb = (Node *) b;
	return pa->a - pb->b;
}
void solve()
{
	qsort(node,N,sizeof(node[0]),cmp);
	int i;
	for(i = 0; i < N - 1; ++ i)
		if(node[i].b > node[i+1].b)
			visit[i] = 1;
	int rear = 0;
	for(i = 0; i < N; ++ i)
		if(!visit[i])
		{
			if(node[i].a >= rear)
			{
				rear = node[i].b;
			}
			else
				visit[i] = 1;
		}
}
void print()
{
	int i;
	for(i = 0; i < N; ++ i)
		if(!visit[i])
			printf("%d %d\n", node[i].a, node[i].b);
}
int main()
{
	freopen("f://data.in","r",stdin);
	init();
	solve();
	print();
	return 0;
}
/*
input:
5
1 5
2 3
3 10
4 8
6 7
*/