Second-词法分析
Second-词法分析
编译器阶段
- 源程序 -> 编译器 -> 目标程序
- 编译器: 前端 -> 中间表示 -> 后端
- 前端: 词法分析器 -> 记号 -> 语法分析器
- 中间表示: 抽象语法树
- 后端: 语义分析器
- 词法分析器: 一段程序代码,主要功能是把字符流转变为记号流
- 词法分析器列子:
- 字符流输入:if (x > 5)
- 词法分析结果:IF LPAREN IDENT(x) GT INT(5) RPAREN
- 词法分析步骤:
- 把字符流转变为编译器内部定义的数据结构,编码所能识别出的词法单元
- 读入i,识别i之后把它转换为数据结构:k=IDENT;lexeme=i;
- 读入f,识别f之后把它转换为数据结构:k=IDENT;lexeme=f;
- 读入空格,转到终态,查表识别关键字,返回关键字:IF;
- 读入(,识别(之后把它转换为数据结构:k=LPAREN;lexeme=nil;
- 读入x,识别x之后把它转换为数据结构:k=IDENT;lexeme=x;
- 读入空格,转到终态,查表识别关键字,返回标识符:IDENT(x);
- ……
- 记号的数据结构定义
enum kind {
IF, LPAREN, ID, ...
};
struct token {
enum kind k;
char *lexeme;
}
词法分析器的实现方法
- 两种方案:
- 手工编码:需要如何转换自己编写代码实现
- 相对复杂、且易于出错
- 目前非常流行的实现方法:GCC,LLVM…
- 词法分析器的生成器:输入其声明式的规范,即可自动生成词法分析器实现代码
- 可快速原型、代码量较少
- 但较难控制细节
- 手工编码:需要如何转换自己编写代码实现
词法分析器的手工编码
状态转换图
- 识别高级语言的单词符号
- 状态转换图算法
token nextToken()
c = getChar();
switch(c)
case '<': c = getChar();
switch(c)
case '=': return LE;
case '>': return NE;
default: rollback();return LT;
case '=': return EQ;
case '>': c = nextChar();
switch(c)
...
- 标识符转换图
- 初始状态下的字符是字母或下划线,转换到1状态,如果是字母或数字或下划线,执行闭包,如果为其他字符则进入终态,返回标记号,回退其他字符到初始态进行下一轮识别
- 关键字表算法
- 对给定语言中所有的关键字,构造关键字构成的哈希表H
- 对所有的标识符合关键字,先统一按标识符的状态转换图进行识别
- 识别完后,进一步查表H看是否是关键字
- 通过合理的构造哈希表H(完美哈希),可以O(1)时间完成
词法分析器的自动生成
正则表达式
- 对状态转换图的概念加以形式化,便于词法分析器的自动生成
- 对给定的字符集∑={c1,c2,c3…,cn}
- 归纳定义:其中前两种是基本,后三种是归纳
- 空串ε是正则表达式
- 对于任意c∈∑,c是正则表达式
- 选择 M|N = {M,N}
- 连接 MN = {mn|m∈M,n∈N}
- 闭包 M* = {ε,M,MM,MMM,…}
- 正则表达式的形式表示,其中前两种是基本,后三种是归纳
1. e -> ε
2. | c (c∈∑)
3. | e | e
4. | e e
5. | e*`- 问题:对于给定字符集∑={a,b},可以写出哪些正则表达式
1. ε
2. a,b
3. ε|ε, ε|a,...
4. εa,εb,ab,εε,a(ε|a),a(ε|b),...
5. (a(ε|a))*,ε闭包...- 例子:关键字 ∑= ASCII
if: i ε ∑, f ε ∑,i与f之间存在一个连接符,连接后依然是正则表达式
int: i ε ∑, n ε ∑,t ε ∑, 它们之间存在两个连接符,由正则表达式的归纳可知它们依然是正则表达式- 例子:标识符
- 用正则表达式表示:(26+26+1)(26+26+10+1)
- (a|b|…|z|A|B|…|Z|下划线)(a|b|…|z|A|B|…|Z|_|1|2|…|0)
- 语法糖:都可以用正则表达式求得,但是比正则表达式容易使用
有限状态自动机(FA)
- 更一般化得状态转换图,分为
DFA和NFA - 输入的字符串 -> FA -> {Yes, No}
- M = (∑,S,q0,F,δ) -> (字母表,状态集,初始状态,终结状态集,转移函数)
- DFA自动机例子: 对于任意的字符,最多有一个状态可以转移
- 字母表:{a,b}
- 状态集:{0,1,2}
- 初始状态:0
- 终结状态集:{2}
- 转移函数:
{(q0,a)->q1,(q0,b)->q0,
(q1,a)->q2,(q1,b)->q1,
(q2,a)->q2,(q2,b)->q2,
...
}- NFA自动机例子: 对于任意的字符,有多于一个状态可以转移
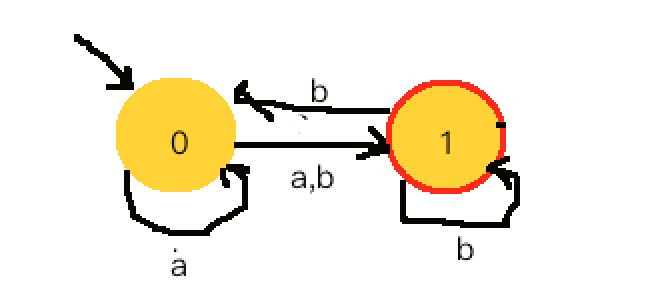
- 字母表:{a,b}
- 状态集:{0,1,}
- 初始状态:0
- 终结状态集:{1}
- 函数转移
{(q0,a)->{q0,q1},
(q0,b)->{q1},
(q1,b)->{q0,q1},
...
}- DFA的实现
RE -> NFA
- 自动生成
- 声明式的规范 -> NFA -> 词法分析器DFA
- RE (Thompson算法)-> NFA(子集构造算法) -> DFA(最小化算法) -> 词法分析器代码
- Thompson算法
- 对基本的RE的直接构造(e -> ε; e -> c)
- 对复合的RE递归构造(复合:a(b|c)*,递归成最基本的再直接构造)
- 例子:a(b|c)*
- 从左到右逐个拆分
- 最后结果M{{a,b,c},{0-9},0,9,δ}
NFA -> DFA
- 子集构造算法
q0 <- eps_closure (n0) //求n0状态的ε_闭包 -> q0 = {n0};
Q <- {q0} // Q = {q0};
workList <- q0
while (workList != []) //当工作表不为空
remove q from workList //取出工作表一个元素
foreach (character c) // 对256个字符做循环
t <- e-closure(delta(q,c)) // 求变节点,再求节点闭包
D[q,c] <- t // (q0,c) -> q1
if (t\not\in Q)
add t to Q and workList // 如果子集合t没有包含在集合Q上,则把它加到Q- 不动点算法,能够运行终止Q={q0,q1,q2,q3,…}元素有限,子集数为2^n
- 最坏情况下的时间复杂度为O(2^n)
- 在实际中不常发生,因为并不是每个子集都会出现
- 算法步骤:
- 在起始状态q0下读入∑里的任意一个字符,能够到达的节点状态,再求该节点的ε_闭包,以上描述的两部分求出的范围便是q1子集
- 在q1子集的元素中读入∑里的任意一个字符,能够到达的节点状态,再求该节点的ε_闭包,以上描述的两部分求出的范围便是q2子集
- 继续求直至没有字母表的字符没有
- Q={q0,q1,q2,q3,…}
- ε_闭包的计算:深度优先,子集首先包括了节点自身
/** 深度优先时间复杂度:O(N) */
// 全局变量,集合,空集
set closure = {};
void eps_closure (x)
closure += {x} // 把x加进集合
forreach (y: x--ε--> y) // x通过边ε到达y
if (!visited(y)) // 如果y没走过,递归走y
eps_closure (y)
// 如果一开始有多个节点,则求多个节点的闭包之后求并集DFA的最小化:简化后的边、状态越少,所需要占用的资源越小
- 算法:Hopcroft:基于等价类的思想
// S:一个状态的集合,split:切分
split(S)
foreach (character c)
if (c can split S)
split S into T1,T2,...,Tk
hopcroft ()
split all nodes into N,A // 把所有切分为两个不可相容的状态,接受和不可接受状态,
while (set is still changes)
split(s)- 例1
- 例2
DFA的代码表示
- 转移表—邻接矩阵:状态、字符
- 哈希表
- 词法分析驱动代码
- 最长匹配
- 跳转表
- 具体选择哪一种要取决于实际中,对时间空间的权衡