图的最小生成树之Prim算法
图的最小生成树是指一颗连接图中所有顶点,具有权重最小的树,树的权重为所有树边的权重之和。最小生成树可以应用在电路规划中,规划出既能连接各个节点又能使材料最为节省的布局。计算最小生成树有两个经典算法,分别是Kruscal算法和Prim算法。本文将会介绍Prim算法的原理以及实现。
Prim算法基于贪心算法设计,其从一个顶点出发,选择这个顶点发出的边中权重最小的一条加入最小生成树中,然后又从当前的树中的所有顶点发出的边中选出权重最小的一条加入树中,以此类推,直到所有顶点都在树中,算法结束。
下面举一个例子来说明。
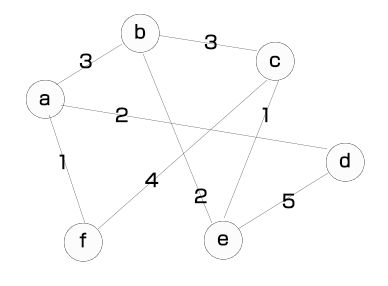
上图是一个无向图,假设我们从顶点a出发使用Prim算法计算最小生成树,其算法运行过程如下。
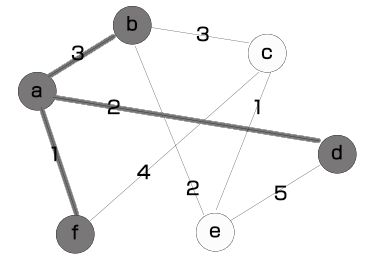
① 顶点a发出的边包括<a,b>和<a,d>和<a,f>,其中权重最小的边为<a,f>,于是我们将边<a,f>加入到最小生成树中,此时最小生成树包括下图中的阴影边和灰色顶点。
② 接下来我们继续从当前最小生成树中的顶点发出的所有边中寻找权重最小的一条,即边<a,b>、<a,d>、<f,c>中的边<a,d>,于是我们将边<a,d>加入到树中,如下图所示。
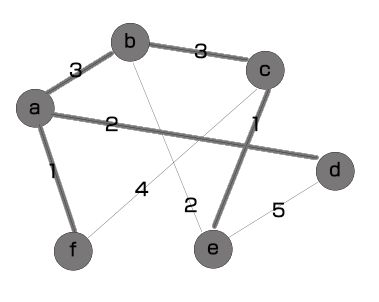
③ 继续上述步骤,从顶点a、f、d发出的边中选出权重最小的一条,即边<a,b>,并将它加入树中,如下图所示。
重复上述步骤,最后得到图的最小生成树如下图所示。
下面给出图的数据结构定义,一如既往,我还是用邻接表来表示图。
typedef struct GNode
{
int number; // 顶点编号
struct GNode *next;
} GNode;
typedef struct Vertex
{
int number;
int weight; // 边(p, v)的权重,用于最小生成树中记录该顶点到已有树的最小距离
int f; // 在prim算法中表示该结点是否已被加入最小生成树中
struct Vertex *p;
} Vertex;
typedef struct Graph
{
GNode *LinkTable;
Vertex *vertex;
int VertexNum;
} Graph;GNode是邻接表的元素结构定义,其记录了顶点的编号。邻接表的表示形式和含义可以参考其它资料,此处不做详述。Vertex是顶点的数据结构定义,其属性number为顶点编号,从1开始,weight是在计算最小生成树的过程中记录该顶点到已有的树的最小距离,f记录其是否已经被加入最小生成树中,p则是其在最小生成树中的父顶点。Graph为图的界都定义。LinkTable为记录边的邻接表,vertex为顶点数组,按顶点编号升序排序,vertexNum是顶点个数。
下面给出基于以上数据结构以及Prim算法实现的最小生成树程序。
// prim算法,输入图g的结点编号从1开始
void prim(Graph *g, int **w, int root)
{
Vertex *vs = g->vertex;
GNode *links = g->LinkTable;
int vertexNum = g->VertexNum;
for (int i = 0; i < vertexNum; i++)
{
(vs + i)->weight = INF;
(vs + i)->p = NULL;
(vs + i)->f = 0;
}
(vs + root - 1)->weight = 0;
while (1)
{
int no = min(vs, vertexNum);
if (no == 0)
{
break;
}
Vertex *u = vs + no - 1;
u->f = 1;
GNode *link = links + no - 1;
link = link->next;
while (link != NULL)
{
int weight = *((int *)w + (no - 1)*vertexNum + link->number - 1);
Vertex *v = vs + link->number - 1;
if (v->f == 0 && weight < v->weight)
{
v->weight = weight;
v->p = u;
}
link = link->next;
}
}
}
int min(Vertex *vs, int num)
{
int min = INT_MAX;
int m = -1;
for (int i = 0; i < num; i++)
{
if ((vs + i)->f == 0 && (vs + i)->weight < min)
{
min = (vs + i)->weight;
m = i;
}
}
return m + 1;
}上述Prim算法需要3个参数,分别是图g,权重矩阵w和树根顶点编号root。其实root给定哪一个编号都不会影响最后的结果。算法首先对所有顶点进行初始化。然后开始循环拾取最小生成树的树边。在每一次循环找到一条树边的时候,计算该树边连接的另一个顶点的所有相邻顶点(有边连接的顶点)距离最小生成树的距离。顶点距离最小生成树的距离定义为该顶点距离树中所有顶点的最小距离。然后再进行下一次循环,直到所有顶点都已经加入到树中。循环会进行V次,V是顶点的个数。
方法min可以从顶点集合中选取距离最小生成树距离最小的顶点。
下面给出一个应用Prim算法的例子。
Graph graph;
graph.VertexNum = 5;
Vertex v[5];
Vertex v1; v1.number = 1; v1.p = NULL; v[0] = v1;
Vertex v2; v2.number = 2; v2.p = NULL; v[1] = v2;
Vertex v3; v3.number = 3; v3.p = NULL; v[2] = v3;
Vertex v4; v4.number = 4; v4.p = NULL; v[3] = v4;
Vertex v5; v5.number = 5; v5.p = NULL; v[4] = v5;
graph.vertex = v;
GNode nodes[5];
GNode n1; n1.number = 1;
GNode n2; n2.number = 2;
GNode n3; n3.number = 3;
GNode n4; n4.number = 4;
GNode n5; n5.number = 5;
GNode a; a.number = 3; GNode b; b.number = 4; GNode y; y.number = 5; n1.next = &a; a.next = &b; b.next = &y; y.next = NULL;
GNode c; c.number = 3; GNode x; x.number = 4; n2.next = &c; c.next = &x; x.next = NULL;
GNode d; d.number = 1; GNode e; e.number = 2; n3.next = &d; d.next = &e; e.next = NULL;
GNode f; f.number = 5; GNode g; g.number = 2; GNode j; j.number = 1; n4.next = &f; f.next = &g; g.next = &j; j.next = NULL;
GNode h; h.number = 4; GNode i; i.number = 1; n5.next = &h; h.next = &i; i.next = NULL;
nodes[0] = n1;
nodes[1] = n2;
nodes[2] = n3;
nodes[3] = n4;
nodes[4] = n5;
graph.LinkTable = nodes;
int w[5][5] = { 0, INF, 4, 2, 5,
INF, 0, 2, 3, INF,
4, 2, 0, INF, INF,
2, 3, INF, 0, 1,
5, INF, INF, 1, 0 };
int root = 1;
prim(&graph, (int **)w, root);
for (int i = 0; i < graph.VertexNum; i++)
{
if (i != root - 1)
{
Vertex *v = graph.vertex + i;
printf("(%d, %d) ", v->p->number, v->number);
}
}上述例程构建了一个图及其权重矩阵,然后调用Prim算法计算树根为顶点1的最小生成树并输出其所有树边。
程序运行结果如下。
本文介绍了计算最小生成树的Prim算法。完整程序可以参考我的github项目 数据结构与算法