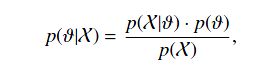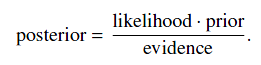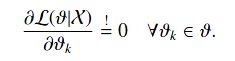参数估计(极大似然估计,极大后验概率估计,贝叶斯估计)
参数估计是学习一主题模型为基础的文本分析的先决条件,很多人直接看PLSA和LDA,看的云里雾里的,因为里面有很多的概率方面的术语和公式,比如likelihood,后验概率,共轭等。学习这些topic model,也不知道应该先去看什么,我认为,首先要看的就是参数估计。
推荐一篇论文:Parameter estimation for text analysis。
参数估计中,我们会遇到两个主要问题:(1)如何去估计参数的value。(2)估计出参数的value之后,如何去计算新的observation的概率,即进行回归分析和预测。
首先定义一些符号:(1)(2)
![]()
![]() (3)
(3)![]()
注意:数据集X中的所有Xi,他们是独立同分布的,因此后面求X 的概率的时候,xi可以相乘。
贝叶斯公式是非常非常重要的,下面进行的所有讨论都是建立的贝叶斯公式的基础之上的:
解释一下这个公式:(1):参数是有一个先验分布的,我们的目的就是基于参数的先验分布和一系列的观察X,推断出当前的参数值。
(2):参数的后验分布。
(3):evidence,即我们要根据这些观察去估计参数的value。
(4):似然概率。
下面我们主要讲三种参数估计的方法:(1)极大似然估计。(2)极大后验概率估计。(3)贝叶斯估计。由易到难,估计的value也越来越perfect。
一.极大似然估计:Maximum likelihood estimation。
极大似然估计相对来说是比较简单的,这个本科的概率论上都学过。这里再简单的说一下。
顾名思义,当然是要找到一个参数,使得最大,为什么要使得它最大呢,因为X都发生了,即基于一个参数发生的,那么当然就得使得它发生的概率最大。
定义似然函数:L(theta|X):
注意:这是一个基于Theta的函数,观察X是已经给定了的。另外上面为什么是相乘的,因为它们之间是独立同分布的。
由于,L函数是多个概率相乘的形式,因此可以使用log(将乘法转化为加法)去简化计算。
求出了似然函数的形式之后,就可以通过求偏导数的方式求出参数值:
说到这里,我们已经求出的参数值,但是这不是最终目的,我们的最终目的是去预测新事件基于这个参数下发生的概率。
注意:注意有一个约等于,因为他进行了一个近似的替换,将theta替换成了估计的值,便于计算。
因此,![]()
举一个例子,加深理解:
未完待续,下一篇再讲极大后验估计。