优化算法——OWL-QN

一、正则化(Regularization)

1、正则化的作用

    在机器学习中，正则化是相对于过拟合出现的一种特征选择的方法。在机器学习算法中使用的Loss项为最小化误差，而最小化误差是为了让我们的模型拟合我们的训练数据，此时，若参数过分拟合我们的训练数据就会形成过拟合的问题，而规则化参数的目的就是为看防止我们的模型过分拟合我们的训练数据。此时，我们会在Loss项之后加上正则项以约束模型中的参数：

 

其中，为损失函数项，为正则项。

2、正则化的种类

    正则化的方法主要有两种：

1. L1正则
2. L2正则

其中，L1正则和L2正则的形式如下：

1. L1正则：
2. L2正则：

其中，为大于0的常数。

3、两种正则化的区别

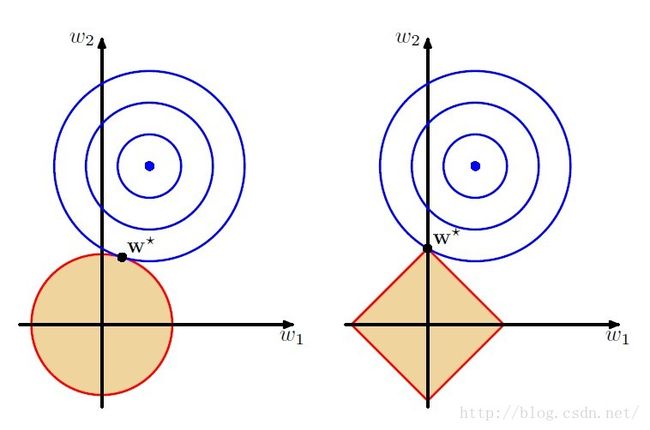
    在很多讲解正则化的材料中都会有如下的一张图

(图片来自：http://www.zhihu.com/question/20700829)

左图是L2正则，右图为L1正则。当模型中只有两个参数，即和时，L2正则的约束空间是一个圆，而L1正则的约束空间为一个正方形，这样，基于L1正则的约束会产生稀疏解，如图所示，即图中某一维()为0。而L2正则只是将参数约束在接近0的很小的区间里，而不会正好为0。对于L1正则产生的稀疏解有很多的好处，如可以起到特征选择的作用，因为有些维的系数为0，说明这些维对于模型的作用很小。

二、OWL-QN算法的思想

1、L1正则的特点

    对于带有L1正则的函数

 

对于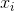，若其符号确定后(即确定变量所在的象限(Orthant))，函数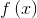即为线性函数，此时的函数是可导的函数。

2、OWL-QN算法的思想

   基于以上L1正则的特点，微软提出了OWL-QN(Orthant-Wise Limited-Memory Quasi-Newton)算法，该算法是基于L-BFGS算法的可用于求解L1正则的算法。简单来讲，OWL-QN算法是指假定变量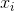的象限确定的条件下使用L-BFGS算法来更新，同时，使得更新前后变量在同一个象限中(使用映射来满足条件)。

三、OWL-QN算法的具体过程

           在OWL-QN算法中，为了使得更新前后的变量在同一个象限中，定义了一些特殊的函数，用于求解L1正则的问题。

1、伪梯度(pseudo-gradient)

 

其中，

 

 

我们重新定义下上述的伪梯度函数：

 

 

其中，。注意上述的伪梯度函数，有下式成立：

 

 

这样就保证了在处取得的方向导数是最小的。

2、映射

   有了函数的下降的方向，接下来必须对变量的所属象限进行限制，目的是使得更新前后变量在同一个象限中，定义函数：

 

上述函数直观的解释是若和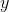在同一象限则取，若两者不在同一象限中，则取0。

3、线搜索

上述的映射是防止生成的新的点的坐标超出象限，而对坐标进行的一个约束，具体的约束的形式如下：

 

 

其中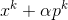，是更新的公式，表示的是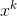所在的象限，具体形式如下：

 

 

表示的是伪梯度下降的方向，其具体形式为：

 

 

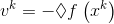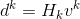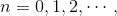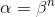其中，，。选择的方式有很多种，前面也介绍了一些，在OWL-QN中，使用了一种backtracking line search的变种，具体如下：选择常数，对于使得满足：

 

 

4、算法流程

参考文献

[1] Scalable Training of L1-Regularized Log-Linear Models