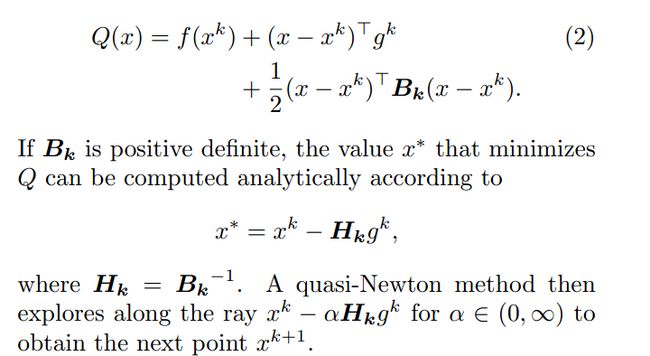OWL-QN算法： 求解L1正则优化

    在机器学习模型中，比如监督学习中，我们设计模型，我们重要的的工作是如何求解这个模型的最优值，通常是如何求救损失函数的最小值。比如logistic regression 中我们求解的是的loss function就是负log 最大似然函数。logistic regression 被广泛应用与互联网应用中，比如反欺诈，广告ctr。logistic regression是广义线性模型，优点是简单，实现容易，线上能很快响应。当数据不是呈现线性关系的时候，如果我们想应用logistic regression就得扩大特征空间，比如做非线性变换，特征组合来达到非线性模型的效果。对于非线性模型比如GDBT， Random Forest，SVM的RBF核，相对就不需要做这些特征变换，因为模型本身已经已经做了非线性工作。我认为，GBDT， Randomn Forest 这种他的非线性方法一个重要的工作就是做特征的组合，而SVM的RBF核只是单一特征变换，做了升维工作，让数据在更高维空间能被划分。在lr模型中特征过多，或者非线性模型中，极容易出现过拟合，为了尽量避免过拟合，同样的做法就是加正则方法。通常的正则方法为L1和L2。L1相对L2有个好处就是，他不仅可以避免过拟合问题，还可以起到特征选择的作用。当loss function 加L1的正则的时候，最优解会使很多不重要的特征收敛到0值，而L2只会把这些特征收敛到一个很小的值，但不是0。 我们来看下一个通用的加上L1的损失函数：

f(x) = l(x) + c||x||, 其中l(x) 是原来的可导损失函数。 

现在的问题是如何求解f(x) 的最小值点。从f(x) 上来看，应为加了L1，导致在x=0点不可导，所以以往直接算梯度的方法就不可取了。Microsoft  Research的人员在ICML2007提出了一种基于L-BFGS的OWL_QN算法来求解因为L1加入带来的不可导问题，具体参考（Andrew G, Gao J. Scalable training of L 1-regularized log-linear models[C]//Proceedings of the 24th international conference on Machine learning. ACM, 2007: 33-40.）。

下面是文献中把求解函数进行泰特展开，如下：

从上面看到，主要涉及到的就是一个一阶梯度，和一个Hessian矩阵。求解hessian矩阵就是这里的挑战。L-BFGS采用有限的空间，牺牲少许精度的方法来求救hession。主要涉及几个一维的向量，具体算法可参考wiki上的。

下面是wiki上关于L-BFGS的算法。

附上这块的部分实现代码：

 while (gnorm > gtol) and (k < maxiter):
        # find search direction (Nocedal & Wright 2006, p.178, Algorithm 7.4)
        q = numpy.array(gfk, dtype=gfk.dtype)
        size = len(sList)
        aList = [None]*size
        if size > 0:
            for i in xrange(size-1,-1,-1):
                aList[i] = rhoList[i] * numpy.dot(sList[i],q)
                q -= aList[i] * yList[i]
            # modify to ensure a well-scaled search direction (N&W 2006, eq. 7.20)
            q *= (rhoList[-1] * numpy.dot(yList[-1],yList[-1]))**(-1)
            for i in xrange(size):
                b = rhoList[i] * numpy.dot(yList[i],q)
                q += sList[i] * (aList[i] - b)
        pk = -q
        # fix non-descent components
        non_descent = numpy.where(pk*gfk>=0)[0]
        pk[non_descent] = 0

OWL- QN 算法是L-BFGS算法的一种变种，求解L1上不可导的问题。OWL-QN相对L-BFGS，其实大多都是一样的，要是按照从代码上来看，也许就是30行左右代码不一样而已。OWL-QL 相对L-BFGS不一样的地方:

（1）每次选取的下一步最有点Xk+1的的象限进行了限制，不允许跨象限，比如之前Xk< 0 , Xk+1是不允许大于0，这种情况只能把Xk+1设为0；

（2）最原始损失函数的梯度了，做了个次梯度修正（加上L1的修正）

这两点，我们从wiki上分先的OWL- QN的python代码上能看到：

（1）

def simple_line_search_owlqn(f, old_fval, xk, pk, gfk, k, Cvec):
    """Backtracking line search for fmin_owlqn. A simple line search works reasonably
    well because the search direction has been rescaled so that the Wolfe conditions
    will usually be satisfied for alpha=1 (see Nocedal & Wright, 2006, Numerical
    Optimization, p. 178). NB: To improve efficiency this routine checks only one of
    the Wolfe conditions. This is appropriate only for convex objectives. If the
    objective is not convex it may lead to non-positive-definite Hessian approximations
    and non-descent search directions. (see Nocedal & Wright 2006, chapters 3 and 6.)
    """
    dirDeriv = numpy.dot(pk,gfk)
    if dirDeriv >= 0:
        sys.stderr.write("Warning: Non-descent direction. Check your gradient.\n")
        return None, None, None
    alpha = 1.0
    backoff = 0.5
    if k == 0:
        alpha = 1.0 / (numpy.dot(pk,pk))**(0.5)
        backoff = 0.1
    c1 = 1e-4
    new_fval = None
    while True:
        new_x = xk + alpha * pk
        crossed_discont = numpy.where(numpy.logical_and(Cvec>0, xk*new_x<0))[0]
        new_x[crossed_discont] = 0
        new_fval = f(new_x) + numpy.dot(Cvec,numpy.absolute(new_x))
        if new_fval <= old_fval + c1 * dirDeriv * alpha:
            break
        alpha *= backoff
        if alpha <= 1e-4:
            return None, None, None
    return alpha, new_fval, new_x

(2) 

  gfkp1 = myfprime(xkp1) # raw loss function gradient;
        # find penalized subgradients
   gfkp1 = subgrad(xkp1,gfkp1,Cvec)

# subgrad：
def subgrad(x, gf, Cvec):
    """Subgradient computation for fmin_owlqn."""
    for i in numpy.where(Cvec>0)[0]:
        if x[i] < 0:
            gf[i] -= Cvec[i]
        elif x[i] > 0:
            gf[i] += Cvec[i]
        else:
            if gf[i] < -Cvec[i]:
                gf[i] += Cvec[i]
            elif gf[i] > Cvec[i]:
                gf[i] -= Cvec[i]
            else:
                gf[i] = 0
    return gf

参考文献：

[1]  Andrew G, Gao J. Scalable training of L 1-regularized log-linear models[C]//Proceedings of the 24th international conference on Machine learning. ACM, 2007: 33-40.

[2] http://en.wikipedia.org/wiki/Limited-memory_BFGS

[3] http://www.umiacs.umd.edu/~msubotin/owlqn.py   . Python implementation by Michael Subotin, intended for use with SciPy