Machine Learning - Andrew NG Class02 - 监督学习应用.梯度下降

问题导读：

1.基本概念

2.梯度下降（Gradient Descent）算法

解决方案：

基本概念

课程中要经常使用的几个符号：

变量定义（符号 Notation）(术语 terminology)：

这里47个房子的 面积-价格的数据集：

• m = Number of training examples （训练样本的数目）
• x’s = “input” variable （表示输入变量）/  features（特征）
• y’s = “output” variable（表示输出变量）  /  “target” variable（目标变量）
• e.g.  (x,y)表示一个trainning example（样本） 而 （xi,yi)表示ith trainning example，也就是样本数据中的第几行.

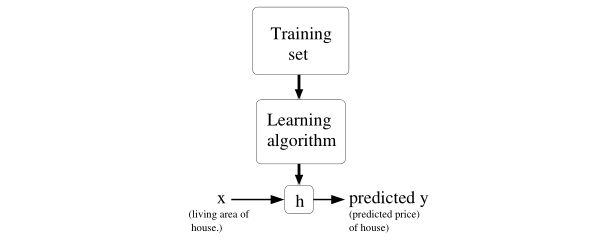
监督学习一般处理流程：

1.  首先找到一个训练集合（Training Set）
2. 将由这个训练集合提供个训练算法（Learning Algorithm）
3. 之后我们要让这个训练算法生成一个输出函数（常用 h 来表示这个函数，这个函数称之为假设[ hypothesis ]）
4. 对于 h 函数，将它 理解为一个x 到 y 上的映射
5. 特征的数目一般被我们表示为 n
6. θ 是一个实数参数，例如，θ 0，θ 1，θ 2   ... 
   

误差函数（cost function）：

• 我们希望算法的预测结果和实际的价格（房价）的平方差最小，用来选取参数theta
• 选择参数theta，以使得参数选取时，能使得预测价格和和实际价格的平方差最小

• 最后求解这个theta，最终使用

Gradient Descent 梯度下降算法

过程：

梯度下降法是按下面的流程进行的：

    1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

    2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

    如图：

这是一个表示参数θ与误差函数J(θ)的关系图，红色的部分是表示J(θ)有着比较高的取值，我们需要的是，能够让J(θ)的值尽量的低。也就是深蓝色的部分。θ0，θ1表示θ向量的两个维度。在上面提到梯度下降法的第一步是给θ给一个初值，假设随机给的初值是在图上的十字点。然后我们将θ按照梯度下降的方向进行调整，就会使得J(θ)往更低的方向进行变化，如图所示，算法的结束将是在θ下降到无法继续下降为止。

梯度下降的最终点可能并不是全局最小点，而是一个局部最小点，如图：

这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会受初始值的影响。

利用数学公式描述梯度下降：

对函数J(θ)求偏导J，

下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

一个很重要的地方值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

 用更简单的数学语言进行描述步骤2是这样的：

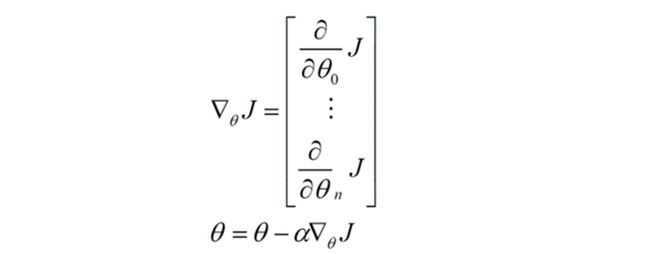
倒三角形表示梯度，按这种方式来表示，θi就不见了，用好向量和矩阵，会大大的简化数学的描述啊。

算法迭代过程：

在linear regression中应用gradient descent没有局部极小值问题，

右图中沿梯度负方向下降，直到左图最小值点，

介绍几种常见的GD算法

1. 批梯度下降（Batch DG）算法
2. 随机梯度下降（stochastic DG）/增量梯度下降 算法
3. 小批量梯度下降算法

博客推荐：

1.梯度下降法的三种形式BGD、SGD以及MBGD

2.随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）的公式对比、实现对比

3. 监督学习应用——线性回归、批梯度下降、随机梯度下降、标准方程推导