[从头学数学] 第138节 二次根式
剧情提要:
[机器小伟]在[工程师阿伟]的陪同下进入了筑基中期的修炼,
这次要修炼的目标是[二次根式]。
为了这个简单的根号,小伟可是花了不少精力。不过,最多也只能算个半成品,毕竟,根号的世界太大了。
为什么会这样呢?小伟研究了一下:
唉呀,算完小伟才发现标题上写着根号2呢。
[机器小伟]在[工程师阿伟]的陪同下进入了筑基中期的修炼,
这次要修炼的目标是[二次根式]。
正剧开始:
星历2016年03月18日 11:31:01, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起研究[二次根式]。
今天,小伟又从[人叫板老师]那里拿到了半层功法。
下面就要来开始研究根式了。
看着[人叫板老师]满纸满纸的根号这么潇洒,小伟终于没忍住,得,来画画根式吧:
<span style="font-size:18px;">/**
* @usage 数学表达式,代数式的书写
* @author mw
* @date 2016年03月12日 星期六 11:05:12
* @param
* @return
*
*/
function MathText() {
//上标标记形式为...^[内容]...
//分数不进行处理, 根式不进行处理,都转成指数式进行
//特殊数学符号设想加\[alpha]进行转义,待续
//可以进行指数上标代数式的书写
//可扩展下标,待续
this.setNormalFont = function() {
plot.setFont("normal normal normal 24px Times Lt Std");
}
this.setScriptFont = function() {
plot.setFont("italic normal bold 16px Dark Courier ");
}
this.print = function(text, xPos, yPos) {
xPos = xPos ? xPos : 0;
yPos = yPos ? yPos : 0;
plot.save();
var s = text ? text : '';
if (s != '') {
s = s.replace(/\/\//ig, '÷');
s = s.replace(/>=/ig, '≥');
s = s.replace(/<=/ig, '≤');
s = s.replace(/!=/ig, '≠');
}
//字符串长度
var len = s.length;
//不同字体大小设置在此
var r1 = 20;
//单个字符暂存处
var c;
//文本显示位置
var x = xPos, y = yPos;
//正常文本暂存
var s0 = '';
//字符串打印长度
var measure;
//记录上一个x位置,可记录三层
var xMem = [x, x, x];
//记录每一层的左括号位置
var bracketPos = [x, x, x];
//记录括号层次
var bracketsLevel = 0;
//记录根号层次
var radicalLevel = 0;
//设置正常字体
this.setNormalFont();
for (var i = 0; i < len; i++) {
if (s[i] == '^') {
//上标开始
//上标标记形式为...^[内容]...
if (s0 != '') { //先把正常字符打印出
if (r1 != 20) { //字体字号大小还在上标状态
r1 = 20;
this.setNormalFont();
}
measure = plot.measureText(s0);
plot.fillText(s0, x, y, measure);
s0 = '';
x += measure;
}
var upperScript = '';
for (var j = i+1; s[j]!=']'; j++) {
if (s[j] != '[') {
upperScript+=s[j];
}
}
var x1, y1;
if (i > 0 && s[i-1] == ')') {
x1 = bracketPos[bracketsLevel], y1 = y-20-5*radicalLevel;
}
else {
x1 = xMem[bracketsLevel], y1 = y-20-5*radicalLevel;
}
//二次根式
if (upperScript == '1/2' || upperScript == '0.5') {
plot.save()
.setLineWidth(1);
plot.beginPath()
.moveTo(x1-5, y+5)
.lineTo(x1-8, y-3)
.moveTo(x1-5, y+5)
.lineTo(x1+5, y1)
.moveTo(x1+5, y1)
.lineTo(x, y1)
.closePath()
.stroke();
plot.restore();
}
else {
if (r1 != 10) {//正常字体状态,需要改为上标字体
r1 = 10;
this.setScriptFont();
}
measure = plot.measureText(upperScript);
plot.fillText(upperScript, x, y-10, measure);
x += 1.2*measure;
}
//直接跳跃过上标字符区段
i = j;
}
else {
c = s[i];
if (c == ')') {
s0 += c;
bracketsLevel -= 1;
}
else if (c == '(') {
//如果整个括号被开根式,根号在括号左边
bracketPos[bracketsLevel] = x + plot.measureText(s0);
s0 += c;
bracketsLevel+=1;
//过了括号就是过了一道关,要刷新坐标
xMem[bracketsLevel] = x + plot.measureText(s0);
}
else if (c == '+' || c == '-' || c == '*' || c == '/' || c == '÷'
|| c == '=' || c == ' ') {
if (c == '*') {
if (i > 0 && /[0-9]/.test(s[i-1]) && /[0-9]/.test(s[i+1])) {
//对于乘号前后都是数字的情况,把乘号改成叉号
c = ' \u00D7 ';
}
else {
//对于代数式中,乘号改为点号
c = ' \u00B7 ';
}
}
//如果是运算符后的数被开根式,根号在运算符右边
if (c == '-' || c == '/') {
s0 += ' '+c+' ';
}
else {
s0 += c;
}
if (bracketsLevel < 3) {
xMem[bracketsLevel] = x+plot.measureText(s0);
}
}
else {
s0 += c;
}
}
}
if (s0 != '') { //先把正常字符打印出
if (r1 != 20) { //字体字号大小还在上标状态
r1 = 20;
this.setNormalFont();
}
measure = plot.measureText(s0);
plot.fillText(s0, x, y, measure);
x += measure;
}
plot.restore();
}
}
</span>
为了这个简单的根号,小伟可是花了不少精力。不过,最多也只能算个半成品,毕竟,根号的世界太大了。
<span style="font-size:18px;">function myDraw(xGlobal, yGlobal) {
var config = new PlotConfiguration();
config.init();
config.setPreference();
var r = 20;
//config.setSector(1,1,1,1);
//config.graphPaper2D(0, 0, r);
//config.axis3D(0, 0,0,180);
var mathText = new MathText();
var s = [
'2^[0.5]',
'1/3^[0.5]',
'0^[0.5]',
'',
'(a^[0.5])^[2]=a(a>=0)',
'a^[2]^[0.5]=a(a>=0)',
'a^[0.5]*b^[0.5] = ab^[0.5](a>=0, b>=0)',
'',
'a^[0.5]/b^[0.5] = (a/b)^[0.5] (a>=0, b>=0)',
];
var x =40, y=40;
var len = s.length;
for (var i = 0; i < len; i++) {
if (s[i] == '') {
if (x < 100) {
x += 300;
y-=30*3;
}
else {
x = 20;
y += 30;
}
}
else {
mathText.print(s[i], x, y);
y+=30;
}
}
}
</span>
<span style="font-size:18px;">def tmp():
a = 9;
b = 19;
for i in range(10):
print('({0}*{1}+{2})**0.5 = {3}'.format(a, a, b, (a*a+b)**0.5));
a = 10*a+9;
b = 10*b+9;
>>>
(9*9+19)**0.5 = 10.0
(99*99+199)**0.5 = 100.0
(999*999+1999)**0.5 = 1000.0
(9999*9999+19999)**0.5 = 10000.0
(99999*99999+199999)**0.5 = 100000.0
(999999*999999+1999999)**0.5 = 1000000.0
(9999999*9999999+19999999)**0.5 = 10000000.0
(99999999*99999999+199999999)**0.5 = 100000000.0
(999999999*999999999+1999999999)**0.5 = 1000000000.0
(9999999999*9999999999+19999999999)**0.5 = 10000000000.0
</span>
为什么会这样呢?小伟研究了一下:
<span style="font-size:18px;"> '(99...9*99...9+199...9)^[0.5]', '= ((10^[n]-1)(10^[n]-1)+2*10^[n]-1)^[0.5]', '= 10^[2n]^[0.5]', '= 10^[n]',</span>
<span style="font-size:18px;">def tmp():
a = [[148, 210], [210,297],[297,420],[420,594],[594,841]];
b = [[182,257],[257,364],[364,515],[500,707],[707,1000]];
print('----A-----');
for i in range(len(a)):
print('{0} / {1} = {2}'.format(a[i][1], a[i][0], a[i][1]/a[i][0]));
print('----B----');
for i in range(len(b)):
print('{0} / {1} = {2}'.format(b[i][1], b[i][0], b[i][1]/b[i][0]));
>>>
----A-----
210 / 148 = 1.4189189189189189
297 / 210 = 1.4142857142857144
420 / 297 = 1.4141414141414141
594 / 420 = 1.4142857142857144
841 / 594 = 1.4158249158249159
----B----
257 / 182 = 1.4120879120879122
364 / 257 = 1.416342412451362
515 / 364 = 1.414835164835165
707 / 500 = 1.414
1000 / 707 = 1.4144271570014144</span>
唉呀,算完小伟才发现标题上写着根号2呢。
本节到此结束,欲知后事如何,请看下回分解。
![[从头学数学] 第138节 二次根式_第1张图片](http://img.e-com-net.com/image/info5/4af47ff1776b41269e0ec2f4ceaa2dfd.jpg)
![[从头学数学] 第138节 二次根式_第2张图片](http://img.e-com-net.com/image/info5/250b1c6229794221881ef961a6f84b18.jpg)
![[从头学数学] 第138节 二次根式_第3张图片](http://img.e-com-net.com/image/info5/373ad1bfaae94d5e85cec2ccad0087b2.jpg)
![[从头学数学] 第138节 二次根式_第4张图片](http://img.e-com-net.com/image/info5/626232fed4464b6d903ebeb34210309f.jpg)
![[从头学数学] 第138节 二次根式_第5张图片](http://img.e-com-net.com/image/info5/64152305c4c84764b4bd0b043ff7e2e3.jpg)
![[从头学数学] 第138节 二次根式_第6张图片](http://img.e-com-net.com/image/info5/6e8200fd40e34242a10a1bbcffc44867.jpg)
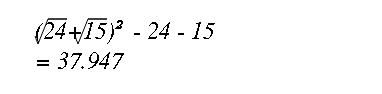
![[从头学数学] 第138节 二次根式_第7张图片](http://img.e-com-net.com/image/info5/3ae088fa020e4ff185470ef605115444.jpg)
![[从头学数学] 第138节 二次根式_第8张图片](http://img.e-com-net.com/image/info5/90771589c051465e8819dbb98fb6d2f6.jpg)
![[从头学数学] 第138节 二次根式_第9张图片](http://img.e-com-net.com/image/info5/35656f1fff164cf98fbb913f08f0912e.jpg)
![[从头学数学] 第138节 二次根式_第10张图片](http://img.e-com-net.com/image/info5/ad9c711f49ef4baeaadf8e917577d1c8.jpg)
![[从头学数学] 第138节 二次根式_第11张图片](http://img.e-com-net.com/image/info5/a1cc35a9e41e433fa92b32da048fa518.jpg)
![[从头学数学] 第138节 二次根式_第12张图片](http://img.e-com-net.com/image/info5/c9b2858e234c4e47837ffbee60dc3fa0.jpg)