数据结构 — 图 之 MPT(最短路径 — dijkstra算法 )
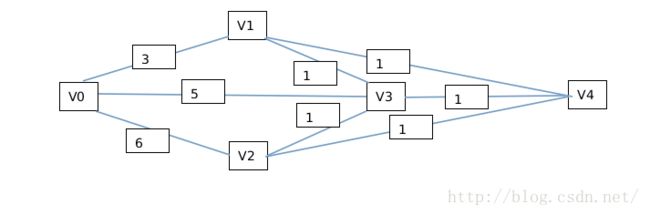
【描述】: 无向图的最短路径 — Dijkstra(适用于非负权值边)
【输入】:
【输出】:
顶点 距离(与源点)
0 0
1 3
2 5
3 4
4 4
/*
Dijkstra(不适用于负权值的边)
*/
#include<iostream>
using namespace std;
/* 宏定义 */
#define INFINITY 65535
#define MAX_NUM 100
#define EleType int
/* 定义一些需要的变量 */
bool visit[MAX_NUM]; //顶点i 是否已经走过了
int dist[MAX_NUM]; //源点到 顶点i 的距离
const int vertices = 5; //顶点数
/* 定义图 */
int graph[vertices][vertices] = {
{ 0,3,6,5,0 },
{ 3,0,0,1,1 },
{ 6,0,0,1,1 },
{ 5,1,1,0,1 },
{ 0,1,1,1,0 }
};
/* 通过dist数组得出得出当下到源点的最小顶点 */
int getMin() {
int min = INFINITY;
int minIndex;
for(int i = 0; i<vertices; i++){
if(!visit[i] && dist[i]<min){
min = dist[i];
minIndex = i;
}
}
return minIndex;
}
/* dijkstra */
void dijkstra(int s){
for(int i = 0; i<vertices; i++){
if(graph[s][i] == 0){
dist[i] = INFINITY;
}else{
dist[i] = graph[s][i];
}
visit[i] = false;
}
//源点距离为0,已经加入SPT
dist[s] = 0;
visit[s] = true;
//更新dist数组
for(int i = 1; i<vertices; i++){
//得到dist数组中的最短距离的顶点
//将其加入SPT
int u = getMin();
visit[u] = true;
//更新
for(int j = 0; j<vertices; j++){
if(!visit[j] && dist[u]!=INFINITY && graph[u][j]!=0 && dist[u]+graph[u][j]<dist[j]){
dist[j] = dist[u]+graph[u][j];
}
}
}
}
/* 输出函数 */
void print() {
cout<<"顶点"<<" "<<"距离(与源点)"<<endl;
for(int i = 0; i<vertices; i++){
cout<<i<<" "<<dist[i]<<endl;
}
}
int main(){
dijkstra(0);
cout<<endl;
print();
return 0;
}