catalan数 + 二叉树 —— POJ 1095
对应POJ题目:点击打开链接
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 7008 | Accepted: 4000 |
Description
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.
The first 10 binary trees and tree number 20 in this sequence are shown below:
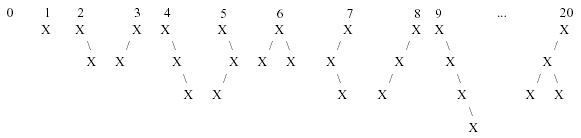
Your job for this problem is to output a binary tree when given its order number.
Input
Output
A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.
Sample Input
1 20 31117532 0
Sample Output
X ((X)X(X))X (X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)
题意:
我们可以用数字来表示唯一的二叉树:
1)空树用编号 0 表示;
2)只有一个结点的树用编号 1 表示;
3)所有含有 m 个结点的二叉树的编号小于含有 m + 1 个结点的二叉树的编号;
4)假如一颗二叉树 T1 有 m 个结点,编号为 n ,左子树的编号为 L,右子树的编号为 R;则要使跟 T1 有相同结点数(即 m )的二叉树 T2 的编号大于 n ,需要满足这两个条件的任意一个:1、T2 的左子树编号大于 L ;2、T2 的左子树编号等于 L,但 T2 的右子树编号大于 R;
思路:
设 f(n) = 有 n 个结点的二叉树一共有多少种表示方法(编号),由乘法原理易知:
f(0) = 1;
f(1) = 1;
f(2) = 2;
f(3) = f(0)*f(2) + f(1)*f(1) + f(2)*f(0) = 5;
f(4) = f(0)*f(3) + f(1)*f(2) + f(2)*f(1) + f(3)*f(0) = 14;
...
所以~这是 catalan 数,可以根据递推公式 f(n) = f(n - 1) * ((4*n - 2) / (n + 1)) 计算出来,记为catalan[]数组;对于一个请求 n :
结点数 m = { j | catalan[0] + catalan[1] + ... + catalan[j] >= n }
在 m 个结点的所有二叉树中编号的排位 pos = n - catalan[0] + catalan[1] + ... + catalan[m-1];
接着是构建二叉树,用递归的思路,我们可以用 BuildTree(m, pos) 来表示构建一颗含有 m 个结点,在 m 个结点的所有二叉树的编号中排位为 pos 的一颗二叉树。如果左子树的结点个数为 i ,则右子树的结点个数为 m - i - 1;我们知道 m个结点的二叉树一共有 f(m) = f(0)*f(m - 1) + f(1)*f(m - 2) + f(2)*f(m - 3) + f(m - 1)*f(0) 个不同的编号;我们需要知道 pos 是在哪个 f(i)*f(m - i - 1) 里面,从而确定左右子树的结点个数进行递归;设 sf(j) = f(0)*f(1) + f(1)*f(m - 2) + ... + f(j)f(m - j - 1) ,则 i = {j | sf(j-1) < pos <= sf(j)}。
用 next_pos 表示 在 f(i)*f(m - i - 1) 种编号中的排位,则 next_pos = pos - sf(i-1);那左子树跟右子树的排位分别是多少呢?可以用类似于进位的思想去想。比如左子树有 2 个结点, 右子树有 3 个结点,则它们一共有 f(2)*f(3) = 10 个编号,next_pos 肯定是 1 ~ 10 的某个数。根据题目意思,它是按右中左的顺序编号的;则我们可以用 next_pos / f(3) 来表示左子树在 f(2) 个编号中的排位 left_pos;用 next_pos % f(3) 来表示右子树在 f(3) 个编号中的排位 right_pos;由于排位要从 1 开始,所以应写成 left_pos = ((next_pos - 1) / f(m - i - 1)) + 1; right_pos = ((next_pos - 1) % f(m - i - 1)) + 1; 最后进行递归调用 BuildTree(i, left_pos) 和 BuildTree(m - i - 1, right_pos) 就可以了。
在递归的过程输出结果就不需要建树。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int catalan[20] = {
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700
};
int sum[20] = {
0, 1, 3, 8, 22, 64, 196, 625, 2055, 6917, 23713, 82499, 290511, 1033411, 3707851, 13402696, 48760366, 178405156, 656043856
};
void BuildTree(int m, int pos)
{
int cnt = 0;
int i, s = 0;
if(0 == m) return;
/*
if(1 == m){
putchar('X');
return;
}
*/
for(i = 0; i < m; i++){
int tmp = catalan[i]*catalan[m-i-1];
if(cnt < pos && pos <= cnt+tmp){
s = pos - cnt;
break;
}
cnt += tmp;
}
if(i){
putchar('(');
BuildTree(i, (s-1)/catalan[m-i-1] + 1);
putchar(')');
}
putchar('X');
if(m - i - 1){
putchar('(');
BuildTree(m - i - 1, (s-1)%catalan[m-i-1]+1);
putchar(')');
}
}
int main()
{
#if 0
freopen("in.txt","r",stdin);
#endif
int n, m, pos;
while(scanf("%d", &n), n){
int i;
for(i = 1; i <= 18; i++)
if(sum[i] >= n){
m = i;
pos = n - sum[m-1];
break;
}
BuildTree(m, pos);
putchar('\n');
}
return 0;
}