POJ 1195 树状数组详解
这题我主要提供树状数组的讲解。
如果想了解为何是lowbit的问题的话,直接从----A----以下开始看
首先还是老图……大家一定见过的……这个图来吓唬一下大家
当然这个图不好看那,我们换个图。
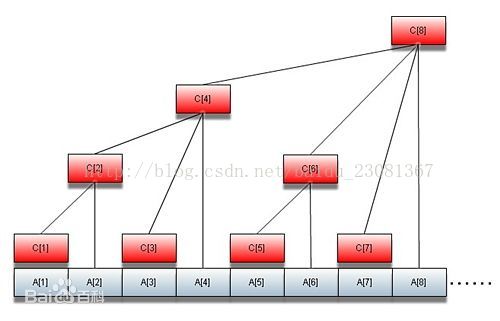
看! 他们看起来就有表示的区间一样。 最低下的,显然是[1, 1] [2,2]之类的区间
倒数第二层的区间,每个区间长度都是2, 倒数第三层长度都是4. (像不像线段树?~~~)
如果这个数据结构,每个节点,都保存了他们的和。 比如[3,3]就是a[3] [4,8]就是a[5]+a[6]+a[7]+a[8]
那么我要求sun(1..9)怎么办? 从图上看,就是[9,9] + [1,8]
要求sum(1..5)呢? [5,5]+[1,4]
要求sum(1..11)呢? [11,11] + [9,10] + [1,8]
也就是说,我们要找到的全部都是从a[i]开始,把图上,i前面所有【最高的】节点的区间和加起来。 【结合上面的例子,要好好理解这句话…… 但是我表达有限了】
(如果不是最高的,是不是要多加好几次?)
现在问题来了,如何总是找i前面“最高的”节点区间呢? 也就是说,我们怎么知道当i=11的时候,要找[11,11] [9,10] [1,8]呢?
=============分割线============
这是一颗很好看的二叉树对不对?
每一个“公共父亲”,
都是每隔1个,出现一次第二层公共父亲 ( [1,1] [2,2]的公共父亲是[1,2] ) 第二层也就是[1,2] [3,4]这些。 也就是在2,4,6,8,10...2k的位置
每隔3个,出现一次第三层共用父亲[1,2] [3,4]的公共父亲是[1,4] 在第三层。 也就是在4,8,12...4k的位置
同理,每隔7个,出现一个第四层共用父亲。 也就是在8,16…… 8k的位置
【能明白我上面的意思了嘛……】
假如【不看图】, 我们考虑11的情况。
我们知道距离11附近有几个点,[1,8]的高度是4,[9,10]的高度是2, 但是!还有[5,8]的高度是3,[7,8]的高度是2。 在10号位置,我们找到最高的,也就是高度为2的[9,10]
在9号点,因为9号已经是[9,10]区间内了,跳过去不考虑。 然后考虑8号位置,8的位置有[1,8]的高度是4,所以选取[1,8]区间。 好了,结束了。 这些区间的并集正好是[1,11]。
但是上述的描述过程,并没有解释如何寻找8,并且又如何知道8的位置有[1,8]的问题……
好了,上面刚才提到,他们“公共父亲”的位置,是和2,4,8这些数字有密切关系……
任何一个数字,都可以是1,2,4,8,16之类的和相加而成。【证明略, 相信大家举例子大概就懂了。 】
……还是不要证明略了……考虑一个数字的二进制,既然都想学树状数组,对二进制数字一定不陌生吧
两个A之间的部分,对二进制大家都很了解了……不了解的再看一下……
----------------------------------------A--------------
9876543210 ( 这一串数字没意义,就是为了和下面的二进制对齐)
二进制 1010010这些数字(这个数字我瞎打的) 他换算成十进制有什么办法呢?
2^6*1 + 2^5 * 0 + 2^4 + 1 + 2^3 *0 + 2^2 *1 + 2*0 * 0。
理解不了?
110101 = 100000+10000+0000+100+00+1 写成这样的二进制形式,大家应该一下子懂了吧。
好了对于二进制化十进制的问题,已经解释了太多了……完全偏题了。
-----------------------A------------
好了,对于110101这个二进制数字, 他拆解成若干个二进制数字之和,就是100000(64)+10000(32)+0000+100(8)+00+1 。
【上面这行给出……其实没啥用,但是我感觉如果说了这句话,很多客官应该顿悟了lowbit的含义为啥是取最后一个1了。 至于想知道为何lowbit是k&-k,仔细想一下补码反码那一块的知识…… 】
假如你初学,完全不知道上面在说什么……没关系,好戏才刚开始。
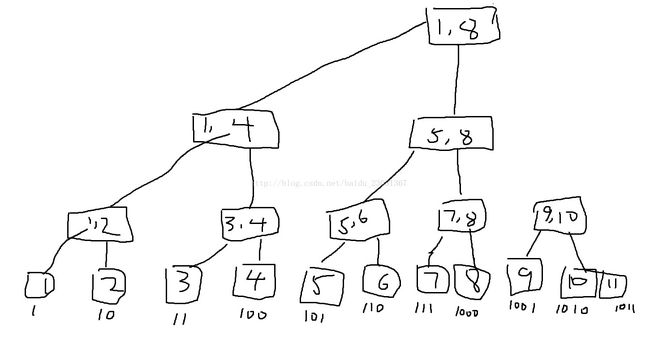
从11开始, 我们考虑11的二进制是1011,说明他是1000(8)+000+10(2) + 1 组成
哎哟你看!我们是不是要找的是 [11,11]对应1 [9,10]对应2(区间长度2) [1,8]区间长度8.
再举个例子1001(9)(你们举个例子推算一下,我就不想写了……)
那么至此,我们已经可以把一个数字,拆解成几个2的整数次幂(我讨厌说这种名词)相加的和。并且这些和从大到小排列的话,可以直接用于题目推算区间的问题。
以11为例,8+2+1。 为何8一定是最高位,如果8不是最高位,假如有2个8,说明有16. 所以8一定是最高位。那么8,一定是一个区间
同理,整个数字都是这样……
================我感觉我语言表达有限,而且我说不清楚了===希望客官已经看懂了,当然看不懂的地方可以提问,我解答的过程也许能把这篇文章写顺了======
好了下面就是所谓的lowbit为何是 k&-k的问题了。
对于8位的情况。
12345678
00010100
这个数字,那么-00010100在计算机是如何表示的?
是最左边是改为1,(符号位) 右边取反, 0变1,1变0,然后+1 即为:
11101011 + 1 = 11101100
00010100
11101100 &运算:
--------------------
00000100
00000100 就把原来数字最右边的1给取出来了~
这个运算过程不懂的,可以先百度百科搜索“补码”。
当然为何这样是对的,这样只是举例子而已……
因为对于一个数字,最右边一大堆数字一定是????1000 (要最右边的1嘛!要不最后一位是1,要不就有若干个0)
???1000因为作为负数,取反后,肯定是???0111
如果再+1. 那么一定是???1000 (因为后面若干个都是连续的0,取反+1,一定会进位到0的位置上去)。 同时因为一定会进位到0上,所以不会再往前进位,1前面的依然是问号。 【一个数字&这个数字取反,一定是0】 所以??? & (取反后的)???,一定全是0. 【 任何数字&0,也一定是0】,所以最后一位1后面的若干个0,&运算后依然是0. 所以 k&-k,可以实现取最后一位。
=====================================
二维树状数组
一维的情况已经说完了,下面说说树状数组如何推广到二维。
因为习惯问题,我习惯这样设置X,Y坐标…… 因为for循环的问题嘛,所以养成这个习惯了。
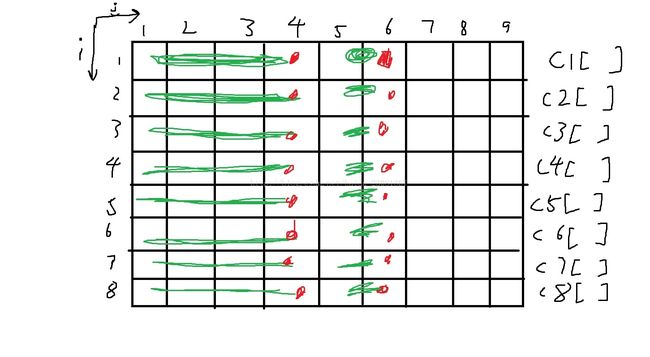
假设c1[]就是这个第一横排, c1数组是一个已经建立好的一维树状数组。
看这个图……(我x,y换成i,j了~ 对于喜欢for (i...) for(j..)的人更习惯一点)
对于横行,6依然和一维的情况一样,表示的是[5,6]区间, 4也依然表示[1,4]区间。 (只列出了4和6的情况,其他情况我偷懒没画)
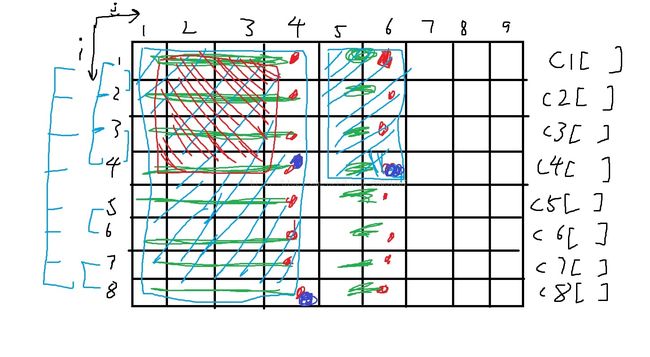
核心大图来了!
这个图说明了i的意思! i=8. j=4,就表示的是左边浅蓝色的整个区间和。
i = 4,j =4,是红色的右斜线区间和。
i =4 j = 6 是右上角浅蓝色的区间和
【这个地方要好好理解】
实际上,就是竖着也被建立了树状数组……
==============================================
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
using namespace std;
#define lowbit(k) ((k)&(-k))
int n;
int a[1030][1030];
void change(int x, int y, int num)
{
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= n; j += lowbit(j))
a[i][j] += num;
}
int ask(int x, int y)
{
int tot = 0;
for (int i = x; i >= 1; i -= lowbit(i))
for (int j = y; j >= 1; j -= lowbit(j))
tot += a[i][j];
return tot;
}
int main()
{
scanf("%d%d",&n, &n);
n += 2;
memset(a, 0, sizeof(a));
int flag;
int x1, y1, x2, y2, tmp;
while (1)
{
scanf("%d", &flag);
if (flag == 1)
{
scanf("%d%d%d", &x1, &y1, &tmp);
x1 += 2, y1 += 2;
change(x1, y1, tmp);
continue;
}
if (flag == 2)
{
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
x1 += 2, y1+=2, x2+=2, y2+=2;
int aa = ask(x2, y2);
int b = ask(x1 - 1, y1 - 1);
int c = ask(x1 - 1, y2);
int d = ask(x2, y1 - 1);
printf("%d\n", b + aa - c -d);
continue;
}
break;
}
return 0;
}