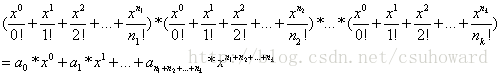poj1521 指数型母函数 整数分式

如果有k个数，每个数有n1，n2，n3...nk个，取出r个，问你有多少种取法。

算法就是利用指数型母函数：

展开式对应的指数为项r的系数就是所求取法。

可以这样理解：对于每个数取多少个，就是取出那个数对应系数的那一项，下面的阶乘是保证可以使取出这些数消去这些数本身的前后顺序。

我的这种写法不知道为什么一直会内存访问出错，我把oj的数据用程序测了一下，发现好像不是数据错误，然后想到可能是程序内存空间不知道怎么就重合了，我就把n、m放到外面，改了这句很奇怪的话就AC了。

（无意间看到队友代码，原来是lld和I64d的问题，在杭电交题要改成I64d，改了以后原来的代码也能AC）

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int MaxN = 15;
LL n, m;
LL a[MaxN], fac[MaxN], ans1[MaxN], ans2[MaxN], mem1[MaxN], mem2[MaxN], tmp1[MaxN], tmp2[MaxN];
void init(){
    fac[0] = fac[1] = 1;
    for(LL i = 2; i < MaxN; i++)
        fac[i] = fac[i-1]*i;
}
LL gcd(LL X, LL Y){return Y?gcd(Y,X%Y):X;}
LL lcm(LL X, LL Y){return X/gcd(X,Y)*Y;}
int main(){
//    freopen("data.in", "r", stdin);
    init();
    while(scanf("%lld%lld", &n, &m) != EOF)
    {
        for(int i = 0; i < n; i++)
        {
            scanf("%lld", &a[i]);
            if(a[i] > m) a[i] = m;
        }
        for(int i = 0; i <= min(a[0], m); i++)
            ans1[i] = 1, ans2[i] = fac[i];
        for(int i = min(a[0], m)+1; i <= m; i++)
            ans1[i] = 0, ans2[i] = 1;
        LL FZ, FM, TMP;
        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j <= m; j++)
                mem1[j] = 0, mem2[j] = 1;
            for(int j = 0; j <= min(a[i], m); j++)
            {
                for(int k = 0; j+k <= m; k++)
                {
                    FZ = ans1[k];
                    FM = ans2[k]*fac[j];
                    TMP = max(gcd(FZ, FM), 1LL);
                    FZ /=TMP, FM /= TMP;

                    TMP = lcm(mem2[j+k], FM);
                    FZ = FZ*(TMP/FM) + mem1[j+k]*(TMP/mem2[j+k]);
                    FM = TMP;
                    TMP = max(gcd(FZ, FM), 1LL);
                    FZ /= TMP, FM /= TMP;
                    mem1[j+k] = FZ, mem2[j+k] = FM;
                }
            }
            for(int j = 0; j <= m; j++)
                ans1[j] = mem1[j], ans2[j] = mem2[j];
        }
        FZ = ans1[m], FM = ans2[m];
        TMP = lcm(fac[m], FM);
        FZ *= TMP/FM;
        printf("%lld\n", FZ);
    }
    return 0;
}