1408070943-hd-还是畅通工程.cpp
克鲁斯卡尔算法(Kruskal's algorithm)是两个经典的最小生成树算法的较为简单理解的一个。这里面充分体现了贪心算法的精髓。大致的流程可以用一个图来表示。这里的图的选择借用了Wikipedia上的那个。非常清晰且直观。
首先第一步,我们有一张图,有若干点和边
如下图所示:
第一步我们要做的事情就是将所有的边的长度排序,用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序,对局部最优的资源进行选择。
排序完成后,我们率先选择了边AD。这样我们的图就变成了
第二步,在剩下的边中寻找。我们找到了CE。这里边的权重也是5
//因为事先将距离排序,所以链接的时候是先将没有连接并且距离最短的相连接,虽然没有挨着连接,但是这样保证了最终距离最短
依次类推我们找到了6,7,7。完成之后,图变成了这个样子。
下一步就是关键了。下面选择那条边呢? BC或者EF吗?都不是,尽管现在长度为8的边是最小的未选择的边。但是他们已经连通了(对于BC可以通过CE,EB来连接,类似的EF可以通过EB,BA,AD,DF来接连)。所以我们不需要选择他们。类似的BD也已经连通了(这里上图的连通线用红色表示了)。
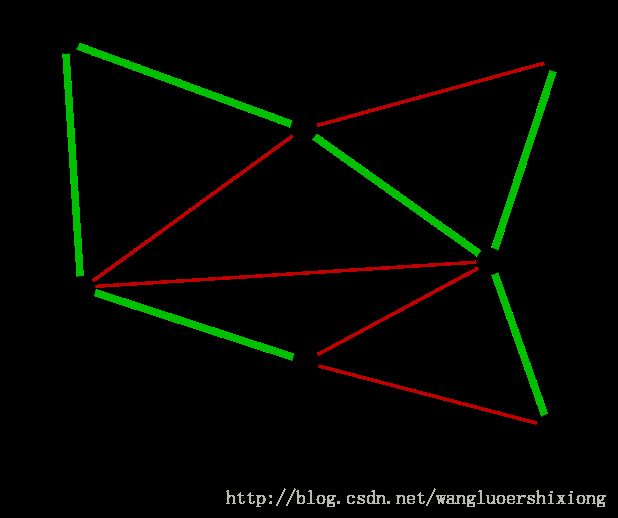
最后就剩下EG和FG了。当然我们选择了EG。最后成功的图就是下图:
到这里所有的边点都已经连通了,一个最小生成树构建完成。
Kruskal算法的时间复杂度由排序算法决定,若采用快排则时间复杂度为O(N log N)。
#include<stdio.h>
#include<algorithm>
using namespace std;
int p[5000];
struct in
{
int x,y,len;
};
in xx[5000];
bool cmp(in a,in b)
{
return a.len<b.len;
}
int find(int a)
{
if(p[a]==a)
return a;
else
return p[a]=find(p[a]);
}
int main()
{
int n,m;
int i,j,k,sum;
while(scanf("%d",&n),n)
{
m=n*(n-1)/2;
for(i=0;i<=n;i++)
p[i]=i; //定义自己跟自己链接
for(i=0;i<m;i++)
scanf("%d%d%d",&xx[i].x,&xx[i].y,&xx[i].len);
sort(xx,xx+m,cmp); //将距离按从小到大排序
sum=0;
for(i=0;i<m;i++)
{
j=find(xx[i].x);
k=find(xx[i].y);
if(j!=k) //若没有建立连接
{
p[j]=k; //则建立连接
sum+=xx[i].len; //两者距离加到总长度
}
}
//因为事先将距离排序,所以链接的时候是先将没有连接并且距离最短的相连接,虽然没有挨着连接,但是这样保证了最终距离最短
printf("%d\n",sum);
}
return 0;
}
#include<algorithm>
using namespace std;
int p[5000];
struct in
{
int x,y,len;
};
in xx[5000];
bool cmp(in a,in b)
{
return a.len<b.len;
}
int find(int a)
{
if(p[a]==a)
return a;
else
return p[a]=find(p[a]);
}
int main()
{
int n,m;
int i,j,k,sum;
while(scanf("%d",&n),n)
{
m=n*(n-1)/2;
for(i=0;i<=n;i++)
p[i]=i; //定义自己跟自己链接
for(i=0;i<m;i++)
scanf("%d%d%d",&xx[i].x,&xx[i].y,&xx[i].len);
sort(xx,xx+m,cmp); //将距离按从小到大排序
sum=0;
for(i=0;i<m;i++)
{
j=find(xx[i].x);
k=find(xx[i].y);
if(j!=k) //若没有建立连接
{
p[j]=k; //则建立连接
sum+=xx[i].len; //两者距离加到总长度
}
}
//因为事先将距离排序,所以链接的时候是先将没有连接并且距离最短的相连接,虽然没有挨着连接,但是这样保证了最终距离最短
printf("%d\n",sum);
}
return 0;
}