试题一
【试题一】
灾区已经非常困难,灾民需要帐篷、衣物、食品和血浆。可通往灾区的道路到处都是塌方,70%以上的路面损坏,桥梁全部被毁。中国空军立即启动应急预案,展开史上最大强度非作战空运行动,准备向灾区空投急需物资。由于余震不断,天气恶劣,怎样知道空投的物资是否落在某灾区的区域内呢?
经过空中观测,某灾区为一凸多边形,空投的物资落在P(X,Y)点。你能否给出一个正确判断?
【标准输入】
第1行: N X Y (N为凸形的边数,X,Y为空投物资的坐标 )
第2行: X1 Y1 X2 Y2…….Xn Yn (逆序给出的N个顶点坐标 )
【标准输出】
YES (物资落在灾区的区域内 )
或
NO (物资落在灾区的区域外 )
【约束条件】
(1) 3 ≤N ≤ 20
(2) 所有的坐标Xi和Yi为整数 -10000≤ Xi ,Yi ≤10000
(3) X,Y为整数 -10000≤ X ,Y ≤10000
(4) 时间限制: 1000MS
【 样 例 】
标准输入
4 2 2
-1 0 3 -2 10 9 -1 110
标准输出
YES
分析:
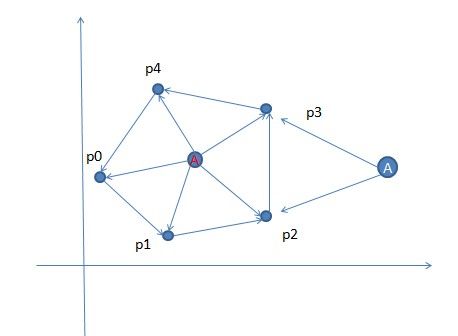
题目分析:求一个给定的点A(x0,y0)是否在凸多边型p0p1...pn-1(逆序给出)内部,我们首先想到的是判断一个三角形三个点是顺时针还是逆时针的,我们可以利用这个结论。
如果点A在多边形内部,则三角形APiP(i+1%n)必为逆时针,而如果在外部,则有些点和A组成的三角形是顺序的,多以,我们只需要依次判断APiP(i+1%n)是否为逆时针即可,一旦发现不是逆时针,则说明在凸多边型外部!
那么我们来看怎么判断三角形的正序还是逆序呢?我们有以下结论:定义向量AB=(x1,y1),AC=(x2,y2),则:
AB X AC>0 逆时针
AB X AC<0 顺时针,其中运算X(向量叉乘)定义为x1*y2-x2*y1。
源程序:
#include <stdio.h>
#define N 25
struct node
{
int x;
int y;
}p[N];
int fun(struct node a,struct node b,struct node c)//向量积
{
int abx,aby,acx,acy,ans;
abx=b.x-a.x;
aby=b.y-a.y;
acx=c.x-a.x;
acy=c.y-a.y;
ans=abx*acy-acx*aby;
if(ans>0) return 1;
else return 0;
}
int main()
{
int i,n,flag;
struct node a,b,c;
while(scanf("%d%d%d",&n,&a.x,&a.y)!=EOF)
{
for(i=0;i<n;i++)
scanf("%d%d",&p[i].x,&p[i].y);
for(i=0,flag=1;i<n;i++)
{
b=p[i];
c=p[(i+1)%n];
flag=fun(a,b,c);
if(flag==0) break;
}
if(flag) printf("YES\n");
else printf("NO\n");
}
return 0;
}