试题五
【试题五】
从5月12日下午地震发生至今已经超过48小时,根据地震救灾的常识推算,未来24小时将是救灾最后的黄金时间。时间在无情的流逝,数以万计的灾民依旧命悬喘息之间。现在,数万军民正日夜奋战在抢救灾民第一线。从人员的组织协调到救灾物资的后援运输,每一个环节都直接关系到救灾的效果好坏。
由于通往各灾区的道路完全中断,大批救援物资只好空投到各个灾区。某军区准备了一批物资, 恰好能均分到处于环形的N个灾区中。遗憾的是,由于余震不断,天气恶劣等原因,落到各灾区的数量不相同。
正如温家宝总理所一再强调的“抢救人的生命,是这次救灾工作的重中之重” 。为了保证救灾的效率不会平白消耗, 当地的民间救助组织可以选择将落到自己所在区的物资传送到左边或者右边相邻的灾区。为了公平起见,我们希望通过相邻灾区的相互传送,最终使所有的灾区获得相同数量的物资。假设一个物资从一个灾区传送到另一个灾区付出的代价是1, 问怎样进行传送,使得所付出的总代价最小。
【标准输入】
第一行: N 表示处于环形的灾区数
接下来n行: 每行一个整数Ai, 表示第i个灾区得到的物质数量。
【标准输出】
输出只有一个数, 表示传送物资付出的最小总代价
【约束条件】
(1) N<=1000000
(2) Ai>=0, 保证Ai在长整型范围内, Ai的总和在int64/long long范围内.
(3)时间限制: 1000MS
【 样 例 】
标准输入
4
4 1 2 5
标准输出
4
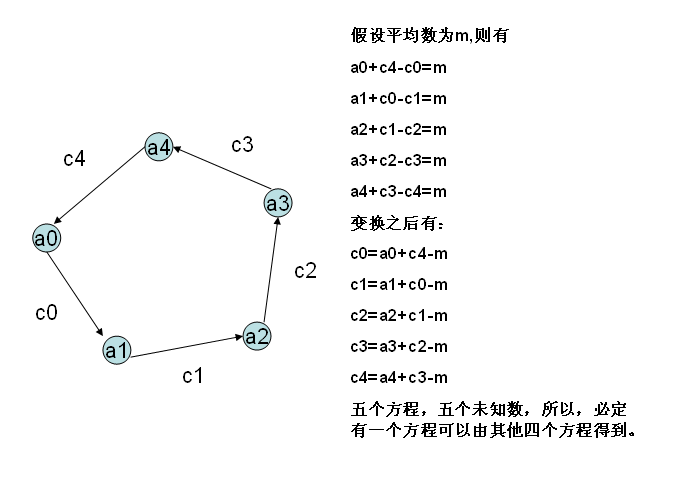
因为任意一个方程都可以由其他四个方程推得,所以可以随意舍弃一个方程,这里我们舍弃方程一,则其他的四个方程都可以由方程一c0表示。那么,我们要求的最小代价就是|c0|+|c1|+|c2|+|c3|+|c4|,这四个点的位置因为c0的取值不同,在X轴上分布的位置也不同(但是c1-c4之间的相对大小不会因为c0取值变化改变而改变),所以,当原点出现在c0-c4的中间位置时,绝对值之和最小,也就是c0,c1,c2,c3,c4的中位数的位置。所以,我们就可以很容易求出来了!
源程序:
#include <iostream>
#include <algorithm>
using namespace std;
#define N 1000010
int a[N+10],c[N+10];
int main()
{
int n,i,j,m,min;
long long sum;
while(cin>>n)
{
for(i=0,sum=0;i<n;i++)
{
cin>>a[i];
sum+=a[i];
}
m=sum/n;
for(i=1,c[0]=0;i<n;i++)
{
c[i]=c[i-1]+a[i]-m;
}
sort(c,c+n);
for(i=0,j=n-1,min=0;i<j;i++,j--)
{
min+=c[j]-c[i];
}
cout<<min<<endl;
}
return 0;
}