深度学习与自然语言处理(4)_斯坦福cs224d 大作业测验1与解答
作业内容翻译:@胡杨([email protected]) && @胥可([email protected])
解答与编排:寒小阳 && 龙心尘
时间:2016年6月
出处:http://blog.csdn.net/han_xiaoyang/article/details/51760923
说明:本文为斯坦福大学CS224d课程的中文版内容笔记,已得到斯坦福大学课程@Richard Socher教授的授权翻译与发表
0 前言
前面一个接一个的Lecture,看得老衲自己也是一脸懵逼,不过你以为你做一个安安静静的美男子(总感觉有勇气做deep learning的女生也是一条汉纸)就能在Stanford这样的学校顺利毕业啦?图样图森破,除掉极高的内容学习梯度,这种顶尖大学的作业和考试一样会让你突(tong)飞(bu)猛(yu)进(sheng)。
说起来,怎么也是堂堂斯坦福的课,这种最看重前言研究在实际工业应用的学校,一定是理论和应用并进,对动手能力要求极强的,于是乎,我们把作业和小测验(MD你这也敢叫小测验!!)也扒过来,整理整理,让大家都来体验体验。反正博主君自己每次折腾完这些大学的assignment之后,都会感慨一句,“还好不生在水生火热的万恶资本主义国家,才能让我大学和研究僧顺利毕业(什么?phd?呵呵…博主是渣渣,智商常年处于欠费状态,我就不参与你们高端人士的趴体了)”。
不能再BB了,直接开始做作业考试吧…
1 Softmax (10 分)
(part a) (5分)
证明针对任何输入向量 x 和常数c,softmax函数的输出不会随着输入向量偏移(也就是常数c)而改变。即:
其中 x+c 就是给 x 每一个元素加上常数c。注意:
提示:在实际应用中,经常会用到这个性质。为了稳定地计算softmax概率,我们会选择 c=−maxixi 。(即将 x 的每个元素减去最大的那个元素)。
博主:熬过了高中,居然又看见证明了,也是惊(ri)喜(le)万(gou)分(le),答案拿来!!!
解答:
证明,针对所有维度 1≤i≤dim(x) :
(part b) (5 分)
已知一个N行d列的输入矩阵,计算每一行的softmax概率。在q1_softmax.py中写出你的实现过程,并使用python q1_softmax.py执行。
要求:你所写的代码应该尽可能的有效并以向量化的形式来实现。非向量化的实现将不会得到满分。
博主:简直要哭晕在厕所了,当年毕业设计也是加论文一星期都可以写完的节奏,这里一个5分的作业,还这么多要求…社会主义好…答案拿来!!!
import numpy as np
def softmax(x):
""" Softmax 函数 """
assert len(x.shape) > 1, "Softmax的得分向量要求维度高于1"
x -= np.max(x, axis=1, keepdims=True)
x = np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
return x2 神经网络基础(30分)
(part a) (3 分)
推导sigmoid函数的导数,并且只以sigmoid函数值的形式写出来(导数的表达式里只包含 σ(x) ,不包含x)。证明针对这个问题没必要单独考虑x。方便回忆:下面给出sigmoid函数形式:
旁白:我年纪轻轻干嘛要走上深度学习这条不归路,真是生无所恋了。
答案: σ′(x)=σ(x)(1−σ(x)) 。
(part b) (3 分)
当使用交叉熵损失来作为评价标准时,推导出损失函数以softmax为预测结果的输入向量 θ 的梯度。注意,
其中 y 是一个one-hot向量, ŷ 是所有类别的预测出的概率向量。(提示:你需要考虑 y 的许多元素为0,并且假设 y 仅有第k个类别是1)
答案: ∂CE(y,ŷ )∂θ=ŷ −y
或者等价于下面表达式,其中假设k是正确的类别
(part c) (6 分)
推导出单隐层神经网络关于输入 x 的梯度(也就是推导出 ∂J∂x ,其中J是神经网络的损失函数)。这个神经网络在隐层和输出层采用了sigmoid激活函数, y 是one-hot编码向量,使用了交叉熵损失。(使用 σ′(x) 作为sigmoid梯度,并且你可以任意为推导过中的中间变量命名)
前向传播方程如下:
在编程问题中,我们假设输入向量(隐层变量和输出概率)始终是一个行向量。此处我们约定,当我们说要对向量使用sigmoid函数时,也就是说要对向量每一个元素使用sigmoid函数。 Wi 和 bi (其中i=1,2)分别是两层的权重和偏移。
旁白:好好的100分总分,硬要被你这么5分6分地拆,人家5分6分是一道选择题,你特么是一整个毕业设计!!好吧,不哭,跪着也要把题目做完,代码写完。哎,博主还是太年轻,要多学习啊。
答案:令 z2=hW2+b2 , z1=xW1+b1x ,于是可得:
(part d) (2 分)
上面所说的这个神经网络有多少个参数?我们可以假设输入是 Dx 维,输出是 Dy ,隐层单元有H个。
旁白:还有part d!!!
答案: (Dx+1)·H+(H+1)·Dy .
(part e) (4 分) 在q2_sigmoid.py中补充写出sigmoid激活函数的和求它的梯度的对应代码。并使用python q2_sigmoid.py进行测试,同样的,测试用例有可能不太详尽,因此尽量检查下自己的代码。
旁白:如果博主没有阵亡,就在走向阵亡的路上…
def sigmoid_grad(f):
""" 计算Sigmoid的梯度 """
#好在我有numpy
f = f * ( 1 - f )
return f(part f) (4 分)
为了方便debugging,我们需要写一个梯度检查器。在q2_gradcheck.py中补充出来,使用python q2_gradcheck.py测试自己的代码。
旁白:做到昏天黑地,睡一觉起来又是一条好汉…
def gradcheck_naive(f, x):
""" 对一个函数f求梯度的梯度检验 - f 输入x,然后输出loss和梯度的函数 - x 就是输入咯 """
rndstate = random.getstate()
random.setstate(rndstate)
fx, grad = f(x)
h = 1e-4
# 遍历x的每一维
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
ix = it.multi_index
old_val = x[ix]
x[ix] = old_val - h
random.setstate(rndstate)
( fxh1, _ ) = f(x)
x[ix] = old_val + h
random.setstate(rndstate)
( fxh2, _ ) = f(x)
numgrad = (fxh2 - fxh1)/(2*h)
x[ix] = old_val
# 比对梯度
reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
if reldiff > 1e-5:
print "Gradient check failed."
print "First gradient error found at index %s" % str(ix)
print "Your gradient: %f \t Numerical gradient: %f" % (grad[ix], numgrad)
return
it.iternext() # Step to next dimension
print "Gradient check passed!"(part g) (8 分)
现在,在q2 neural.py中,写出只有一个隐层且激活函数为sigmoid的神经网络前向和后向传播代码。使用python q2_neural.py测试自己的代码。
旁白:一入DL深似海…
def forward_backward_prop(data, labels, params, verbose = False):
""" 2个隐层的神经网络的前向运算和反向传播 """
if len(data.shape) >= 2:
(N, _) = data.shape
### 展开每一层神经网络的参数
t = 0
W1 = np.reshape(params[t:t+dimensions[0]*dimensions[1]], (dimensions[0], dimensions[1]))
t += dimensions[0]*dimensions[1]
b1 = np.reshape(params[t:t+dimensions[1]], (1, dimensions[1]))
t += dimensions[1]
W2 = np.reshape(params[t:t+dimensions[1]*dimensions[2]], (dimensions[1], dimensions[2]))
t += dimensions[1]*dimensions[2]
b2 = np.reshape(params[t:t+dimensions[2]], (1, dimensions[2]))
### 前向运算
# 第一个隐层做内积
a1 = sigmoid(data.dot(W1) + b1)
# 第二个隐层做内积
a2 = softmax(a1.dot(W2) + b2)
cost = - np.sum(np.log(a2[labels == 1]))/N
### 反向传播
# Calculate analytic gradient for the cross entropy loss function
grad_a2 = ( a2 - labels ) / N
# Backpropagate through the second latent layer
gradW2 = np.dot( a1.T, grad_a2 )
gradb2 = np.sum( grad_a2, axis=0, keepdims=True )
# Backpropagate through the first latent layer
grad_a1 = np.dot( grad_a2, W2.T ) * sigmoid_grad(a1)
gradW1 = np.dot( data.T, grad_a1 )
gradb1 = np.sum( grad_a1, axis=0, keepdims=True )
if verbose: # Verbose mode for logging information
print "W1 shape: {}".format( str(W1.shape) )
print "W1 gradient shape: {}".format( str(gradW1.shape) )
print "b1 shape: {}".format( str(b1.shape) )
print "b1 gradient shape: {}".format( str(gradb1.shape) )
### 梯度拼起来
grad = np.concatenate((gradW1.flatten(), gradb1.flatten(), gradW2.flatten(), gradb2.flatten()))
return cost, grad3 word2vec(40分+5附加分)
(part a) (3分)
假设你得到一个关联到中心词 c 的预测词向量 υc ,并且这个词向量使用skip-gram方法生成,预测词使用的是softmax预测函数,它能够在word2vec模型中被找到。
式中, w 代表第w个词, μw(w=1,…,W) 是词库中全体词汇的输出词向量。假设为交叉熵损失函数,且词 o 是被预测的词汇(noe-hot/独热模型的标记向量中第 o 个元素为1),求解预测词向量 υc 的所对应的梯度。
提示:问题2中的标记法将有助于此问题的解答。比如:设 ŷ 为各个词汇使用softmax函数预测得到的向量, y 为期望词向量,而损失函数可以表示为:
其中, U=[μ1,μ2,…,μW] 是全体输出向量形成的矩阵,确保你已经规定好你的向量和矩阵的方向。
旁边:是的,旁白我已经不知道写什么了,感谢党感谢祖国吧。
解答:设 ŷ 为词汇softmax预测结果的列向量, y 是同样形为列向量的独热标签,那么有:
或者等同于:
(part b) (3分)
条件仍然如前一题所描述,求解输出词向量 μw 的梯度(包括 μo 在内)
旁白:我还是安安静静在天朝搬砖吧
解答:
或者等同于:
(part c) (6分)
仍然延续(part a)和(part b),假设我们使用为预测的向量 υc 使用负采样损失的计算方式,并且设定期望输出词为 o 。假设获得了 K 个负样例(词),并且被记为 1,…,K ,分别作为这些样例的标签 (o∉1,…,K) 。那么,对于一个给定的词 o ,将其输出向量记作 μo 。这里,负采样损失函数如下:
其中, σ(⋅) 为sigmoid激活函数。
当你完成上述操作之后,尝试简要描述这个损失函数比softmax-CE损失函数计算更为有效的原因(你可以给出递增式的学习率,即,给出softmax-CE损失函数的计算时间除以负采样损失函数的计算时间的结果)。
注释:由于我们打算计算目标函数的最小值而不是最大值,这里提到的损失函数与Mikolov等人最先在原版论文中描述的正好相反。
旁白:突然想起来,小时候好焦虑,长大后到底去清华还是去北大,后来发现多虑了。我想如果当初走了狗屎运进了贵T大贵P大,也一定完不成学业。
解答:
(part d) (8分)
试得到由skip-gram和CBOW算法分别算出的全部词向量的梯度,前提步骤和词内容集合[wordc-m,…,wordc-1,wordc,wordc+1,…,wordc+m]都已给出,其中, m 是窗口的大小。将词 wordk 的输入和输出词向量分别记为 υk 和 μk 。
提示:可以随意使用函数 F(o,υc) (其中 o 代表词汇)作为这一部分中 Jsoftmax−CE(o,υc,…) 或 Jneg−sample(o,υc,…) 损失函数的占位符——你将在编程部分看到一个非常有用的抽象类,那意味着你的解决方法可以用这样的形式表达: ∂F(o,υc)∂…
回忆skip-gram算法,以 c 为中心周边内容的损失值计算如下:
其中, wc+j 代表距离中心词的第j个词。
CBOW略有不同,不同于使用 υc 作为预测向量,我们以 υ̂ 为底,在CBOW中(一个小小的变体),我们计算上下文输入词向量的和:
于是,CBOW的损失函数定义为:
注释:为了符合 υ̂ 在诸如代码部分中的各种表达规范,在skip-gram方法中,令: υ̂ =υc 。
旁白:我诚实一点,这个部分真的是烦了课件抄下来的。
解答:为了表达得更为清晰,我们将词库中全部词汇的全部输出向量集合记作 U ,给定一个损失函数 F ,我们可以很容易获得以下引出结果:
∂F(wi,υ̂ )∂U 和 ∂F(wi,υ̂ )∂υ̂
对于skip-gram方法,一个内容窗口的损失梯度为:
同样地,对于CBOW则有:
(part e) (12分)
在这一部分,你将实现word2vec模型,并且使用随机梯度下降方法(SGD)训练属于你自己的词向量。首先,在代码q3_word2vec.py中编写一个辅助函数对矩阵中的每一行进行归一化。同样在这个文件中,完成对softmax、负采样损失函数以及梯度计算函数的实现。然后,完成面向skip-gram的梯度损失函数。当你完成这些的时候,使用命令:python q3_word2vec.py对编写的程序进行测试。
注释:如果你选择不去实现CBOW(h部分),只需简单地删除对NotImplementedError错误的捕获即可完成你的测试。
旁白:前方高能预警,代码量爆炸了!
import numpy as np
import random
from q1_softmax import softmax
from q2_gradcheck import gradcheck_naive
from q2_sigmoid import sigmoid, sigmoid_grad
def normalizeRows(x):
""" 行归一化函数 """
N = x.shape[0]
x /= np.sqrt(np.sum(x**2, axis=1)).reshape((N,1)) + 1e-30
return x
def test_normalize_rows():
print "Testing normalizeRows..."
x = normalizeRows(np.array([[3.0,4.0],[1, 2]]))
# 结果应该是 [[0.6, 0.8], [0.4472, 0.8944]]
print x
assert (np.amax(np.fabs(x - np.array([[0.6,0.8],[0.4472136,0.89442719]]))) <= 1e-6)
print ""
def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
""" word2vec的Softmax损失函数 """
# 输入:
# - predicted: 预测词向量的numpy数组
# - target: 目标词的下标
# - outputVectors: 所有token的"output"向量(行形式)
# - dataset: 用来做负例采样的,这里其实没用着
# 输出:
# - cost: 输出的互熵损失
# - gradPred: the gradient with respect to the predicted word
# vector
# - grad: the gradient with respect to all the other word
# vectors
probabilities = softmax(predicted.dot(outputVectors.T))
cost = -np.log(probabilities[target])
delta = probabilities
delta[target] -= 1
N = delta.shape[0]
D = predicted.shape[0]
grad = delta.reshape((N,1)) * predicted.reshape((1,D))
gradPred = (delta.reshape((1,N)).dot(outputVectors)).flatten()
return cost, gradPred, grad
def negSamplingCostAndGradient(predicted, target, outputVectors, dataset, K=10):
""" Word2vec模型负例采样后的损失函数和梯度 """
grad = np.zeros(outputVectors.shape)
gradPred = np.zeros(predicted.shape)
indices = [target]
for k in xrange(K):
newidx = dataset.sampleTokenIdx()
while newidx == target:
newidx = dataset.sampleTokenIdx()
indices += [newidx]
labels = np.array([1] + [-1 for k in xrange(K)])
vecs = outputVectors[indices,:]
t = sigmoid(vecs.dot(predicted) * labels)
cost = -np.sum(np.log(t))
delta = labels * (t - 1)
gradPred = delta.reshape((1,K+1)).dot(vecs).flatten()
gradtemp = delta.reshape((K+1,1)).dot(predicted.reshape(
(1,predicted.shape[0])))
for k in xrange(K+1):
grad[indices[k]] += gradtemp[k,:]
t = sigmoid(predicted.dot(outputVectors[target,:]))
cost = -np.log(t)
delta = t - 1
gradPred += delta * outputVectors[target, :]
grad[target, :] += delta * predicted
for k in xrange(K):
idx = dataset.sampleTokenIdx()
t = sigmoid(-predicted.dot(outputVectors[idx,:]))
cost += -np.log(t)
delta = 1 - t
gradPred += delta * outputVectors[idx, :]
grad[idx, :] += delta * predicted
return cost, gradPred, grad
def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient = softmaxCostAndGradient):
""" Skip-gram model in word2vec """
# skip-gram模型的实现
# 输入:
# - currrentWord: 当前中心词所对应的串
# - C: 上下文大小(词窗大小)
# - contextWords: 最多2*C个词
# - tokens: 对应词向量中词下标的字典
# - inputVectors: "input" word vectors (as rows) for all tokens
# - outputVectors: "output" word vectors (as rows) for all tokens
# - word2vecCostAndGradient: the cost and gradient function for a prediction vector given the target word vectors, could be one of the two cost functions you implemented above
# 输出:
# - cost: skip-gram模型算得的损失值
# - grad: 词向量对应的梯度
currentI = tokens[currentWord]
predicted = inputVectors[currentI, :]
cost = 0.0
gradIn = np.zeros(inputVectors.shape)
gradOut = np.zeros(outputVectors.shape)
for cwd in contextWords:
idx = tokens[cwd]
cc, gp, gg = word2vecCostAndGradient(predicted, idx, outputVectors, dataset)
cost += cc
gradOut += gg
gradIn[currentI, :] += gp
return cost, gradIn, gradOut
def word2vec_sgd_wrapper(word2vecModel, tokens, wordVectors, dataset, C, word2vecCostAndGradient = softmaxCostAndGradient):
batchsize = 50
cost = 0.0
grad = np.zeros(wordVectors.shape)
N = wordVectors.shape[0]
inputVectors = wordVectors[:N/2,:]
outputVectors = wordVectors[N/2:,:]
for i in xrange(batchsize):
C1 = random.randint(1,C)
centerword, context = dataset.getRandomContext(C1)
if word2vecModel == skipgram:
denom = 1
else:
denom = 1
c, gin, gout = word2vecModel(centerword, C1, context, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient)
cost += c / batchsize / denom
grad[:N/2, :] += gin / batchsize / denom
grad[N/2:, :] += gout / batchsize / denom
return cost, grad
def test_word2vec():
# Interface to the dataset for negative sampling
dataset = type('dummy', (), {})()
def dummySampleTokenIdx():
return random.randint(0, 4)
def getRandomContext(C):
tokens = ["a", "b", "c", "d", "e"]
return tokens[random.randint(0,4)], [tokens[random.randint(0,4)] \
for i in xrange(2*C)]
dataset.sampleTokenIdx = dummySampleTokenIdx
dataset.getRandomContext = getRandomContext
random.seed(31415)
np.random.seed(9265)
dummy_vectors = normalizeRows(np.random.randn(10,3))
dummy_tokens = dict([("a",0), ("b",1), ("c",2),("d",3),("e",4)])
print "==== Gradient check for skip-gram ===="
gradcheck_naive(lambda vec: word2vec_sgd_wrapper(skipgram, dummy_tokens, vec, dataset, 5), dummy_vectors)
gradcheck_naive(lambda vec: word2vec_sgd_wrapper(skipgram, dummy_tokens, vec, dataset, 5, negSamplingCostAndGradient), dummy_vectors)
print "\n==== Gradient check for CBOW ===="
gradcheck_naive(lambda vec: word2vec_sgd_wrapper(cbow, dummy_tokens, vec, dataset, 5), dummy_vectors)
gradcheck_naive(lambda vec: word2vec_sgd_wrapper(cbow, dummy_tokens, vec, dataset, 5, negSamplingCostAndGradient), dummy_vectors)
print "\n=== Results ==="
print skipgram("c", 3, ["a", "b", "e", "d", "b", "c"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset)
print skipgram("c", 1, ["a", "b"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset, negSamplingCostAndGradient)
print cbow("a", 2, ["a", "b", "c", "a"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset)
print cbow("a", 2, ["a", "b", "a", "c"], dummy_tokens, dummy_vectors[:5,:], dummy_vectors[5:,:], dataset, negSamplingCostAndGradient)
if __name__ == "__main__":
test_normalize_rows()
test_word2vec()(f) (4分) 在代码q3_sgd.py中完成对随即梯度下降优化函数的实现。并且在该代码中运行测试你的实现。
旁白:想到这篇文章有可能会被无数可以智商碾压我的大神看到,就脸一阵发烫。
# 实现随机梯度下降
# 随机梯度下降每1000轮,就保存一下现在训练得到的参数
SAVE_PARAMS_EVERY = 1000
import glob
import os.path as op
import cPickle as pickle
import sys
def load_saved_params():
""" 载入之前的参数以免从头开始训练 """
st = 0
for f in glob.glob("saved_params_*.npy"):
iter = int(op.splitext(op.basename(f))[0].split("_")[2])
if (iter > st):
st = iter
if st > 0:
with open("saved_params_%d.npy" % st, "r") as f:
params = pickle.load(f)
state = pickle.load(f)
return st, params, state
else:
return st, None, None
def save_params(iter, params):
with open("saved_params_%d.npy" % iter, "w") as f:
pickle.dump(params, f)
pickle.dump(random.getstate(), f)
def sgd(f, x0, step, iterations, postprocessing = None, useSaved = False, PRINT_EVERY=10, ANNEAL_EVERY = 20000):
""" 随机梯度下降 """
###########################################################
# 输入
# - f: 需要最优化的函数
# - x0: SGD的初始值
# - step: SGD的步长
# - iterations: 总得迭代次数
# - postprocessing: 参数后处理(比如word2vec里需要对词向量做归一化处理)
# - PRINT_EVERY: 指明多少次迭代以后输出一下状态
# 输出:
# - x: SGD完成后的输出参数 #
###########################################################
if useSaved:
start_iter, oldx, state = load_saved_params()
if start_iter > 0:
x0 = oldx;
step *= 0.5 ** (start_iter / ANNEAL_EVERY)
if state:
random.setstate(state)
else:
start_iter = 0
x = x0
if not postprocessing:
postprocessing = lambda x: x
expcost = None
for iter in xrange(start_iter + 1, iterations + 1):
cost, grad = f(x)
x = x - step * grad
x = postprocessing(x)
if iter % PRINT_EVERY == 0:
print "Iter#{}, cost={}".format(iter, cost)
sys.stdout.flush()
if iter % SAVE_PARAMS_EVERY == 0 and useSaved:
save_params(iter, x)
if iter % ANNEAL_EVERY == 0:
step *= 0.5
return x(part g) (4分)
开始秀啦!现在我们将要载入真实的数据并使用你已经实现的手段训练词向量!我们将使用Stanford Sentiment Treebank (SST)数据集来进行词向量的训练,之后将他们应用到情感分析任务中去。在这一部分中,无需再编写更多的代码;只需要运行命令python q3 run.py即可。
注释:训练过程所占用的时间可能会很长,这取决于你所实现的程序的效率(一个拥有优异效率的实现程序大约需要占用1个小时)。努力去接近这个目标!
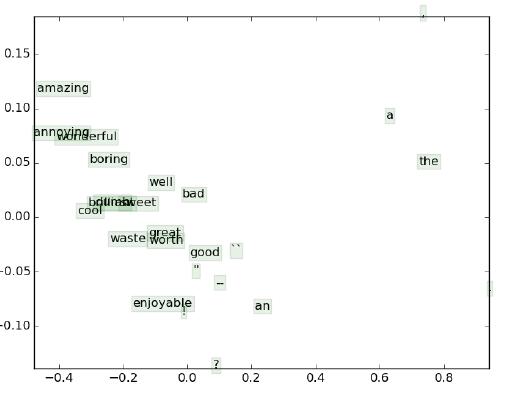
当脚本编写完成,需要完成对词向量的可视化显示。相应的结果同样被保存下来,如项目目录中的图片q3 word_vectors.png所示。包括在你作业中绘制的坐标图。简明解释最多三个句子在你的坐标图中的显示状况。
解答:
(part h) 附加题(5分)
在代码q3_word2vec.py中完成对CBOW的实现。注释:这部分内容是可选的,但是在d部分中关于CBOW的梯度推导在这里并不适用!
def cbow(currentWord, C, contextWords, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient = softmaxCostAndGradient):
""" word2vec的CBOW模型 """
cost = 0
gradIn = np.zeros(inputVectors.shape)
gradOut = np.zeros(outputVectors.shape)
D = inputVectors.shape[1]
predicted = np.zeros((D,))
indices = [tokens[cwd] for cwd in contextWords]
for idx in indices:
predicted += inputVectors[idx, :]
cost, gp, gradOut = word2vecCostAndGradient(predicted, tokens[currentWord], outputVectors, dataset)
gradIn = np.zeros(inputVectors.shape)
for idx in indices:
gradIn[idx, :] += gp
return cost, gradIn, gradOut4 情感分析(20分)
现在,随着词向量的训练,我们准备展示一个简单的情感分析案例。随着词向量的训练,我们准备展示一个简单的情感分析。对于每条Stanford Sentiment Treebank数据集中的句子,将句子中全体词向量的平均值算作其特征值,并试图预测所提句子中的情感层次。短语的情感层次使用真实数值在原始数据集中表示,并被我们用以下5个类别来表示:
对其分别进行从0到4的编码。在这一部分,你将学习用SGD来训练一个softmax回归机,并且通过不断地训练/调试验证来提高回归机的泛化能力。
(part a)(10分)
实现一个句子的特征生成器和softmax回归机。在代码q4_softmaxreg.py中完成对这个任务的实现,并运行命令python q4_ softmaxreg.py,对刚才完成的功能函数进行调试。
import numpy as np
import random
from cs224d.data_utils import *
from q1_softmax import softmax
from q2_gradcheck import gradcheck_naive
from q3_sgd import load_saved_params
def getSentenceFeature(tokens, wordVectors, sentence):
""" 简单粗暴的处理方式,直接对句子的所有词向量求平均做为情感分析的输入 """
# 输入:
# - tokens: a dictionary that maps words to their indices in the word vector list
# - wordVectors: word vectors (each row) for all tokens
# - sentence: a list of words in the sentence of interest
# 输出:
# - sentVector: feature vector for the sentence
sentVector = np.zeros((wordVectors.shape[1],))
indices = [tokens[word] for word in sentence]
sentVector = np.mean(wordVectors[indices, :], axis=0)
return sentVector
def softmaxRegression(features, labels, weights, regularization = 0.0, nopredictions = False):
""" Softmax Regression """
# 完成加正则化的softmax回归
# 输入:
# - features: feature vectors, each row is a feature vector
# - labels: labels corresponding to the feature vectors
# - weights: weights of the regressor
# - regularization: L2 regularization constant
# 输出:
# - cost: cost of the regressor
# - grad: gradient of the regressor cost with respect to its weights
# - pred: label predictions of the regressor (you might find np.argmax helpful)
prob = softmax(features.dot(weights))
if len(features.shape) > 1:
N = features.shape[0]
else:
N = 1
# A vectorized implementation of 1/N * sum(cross_entropy(x_i, y_i)) + 1/2*|w|^2
cost = np.sum(-np.log(prob[range(N), labels])) / N
cost += 0.5 * regularization * np.sum(weights ** 2)
grad = np.array(prob)
grad[range(N), labels] -= 1.0
grad = features.T.dot(grad) / N
grad += regularization * weights
if N > 1:
pred = np.argmax(prob, axis=1)
else:
pred = np.argmax(prob)
if nopredictions:
return cost, grad
else:
return cost, grad, pred
def accuracy(y, yhat):
""" Precision for classifier """
assert(y.shape == yhat.shape)
return np.sum(y == yhat) * 100.0 / y.size
def softmax_wrapper(features, labels, weights, regularization = 0.0):
cost, grad, _ = softmaxRegression(features, labels, weights,
regularization)
return cost, grad
def sanity_check():
""" Run python q4_softmaxreg.py. """
random.seed(314159)
np.random.seed(265)
dataset = StanfordSentiment()
tokens = dataset.tokens()
nWords = len(tokens)
_, wordVectors0, _ = load_saved_params()
wordVectors = (wordVectors0[:nWords,:] + wordVectors0[nWords:,:])
dimVectors = wordVectors.shape[1]
dummy_weights = 0.1 * np.random.randn(dimVectors, 5)
dummy_features = np.zeros((10, dimVectors))
dummy_labels = np.zeros((10,), dtype=np.int32)
for i in xrange(10):
words, dummy_labels[i] = dataset.getRandomTrainSentence()
dummy_features[i, :] = getSentenceFeature(tokens, wordVectors, words)
print "==== Gradient check for softmax regression ===="
gradcheck_naive(lambda weights: softmaxRegression(dummy_features,
dummy_labels, weights, 1.0, nopredictions = True), dummy_weights)
print "\n=== Results ==="
print softmaxRegression(dummy_features, dummy_labels, dummy_weights, 1.0)
if __name__ == "__main__":
sanity_check()(part b)(2分)
解释当分类语料少于三句时为什么要引入正则化(实际上在大多数机器学习任务都这样)。
解答:为了避免训练集的过拟合以及对未知数据集的适应力不佳现象。
(part c)(4分)
在q4 sentiment.py中完成超参数的实现代码从而获取“最佳”的惩罚因子。你是如何选择的?报告你的训练、调试和测试精度,在最多一个句子中校正你的超参数选定方法。 注释:在开发中应该获取至少30%的准确率。
解答:参考值为1e-4,在调试、开发和测试过程中准确率分别为29.1%,31.4%和27.6%
import numpy as np
import matplotlib.pyplot as plt
from cs224d.data_utils import *
from q3_sgd import load_saved_params, sgd
from q4_softmaxreg import softmaxRegression, getSentenceFeature, accuracy, softmax_wrapper
# 试试不同的正则化系数,选最好的
REGULARIZATION = [0.0, 0.00001, 0.00003, 0.0001, 0.0003, 0.001, 0.003, 0.01]
# 载入数据集
dataset = StanfordSentiment()
tokens = dataset.tokens()
nWords = len(tokens)
# 载入预训练好的词向量
_, wordVectors0, _ = load_saved_params()
wordVectors = (wordVectors0[:nWords,:] + wordVectors0[nWords:,:])
dimVectors = wordVectors.shape[1]
# 载入训练集
trainset = dataset.getTrainSentences()
nTrain = len(trainset)
trainFeatures = np.zeros((nTrain, dimVectors))
trainLabels = np.zeros((nTrain,), dtype=np.int32)
for i in xrange(nTrain):
words, trainLabels[i] = trainset[i]
trainFeatures[i, :] = getSentenceFeature(tokens, wordVectors, words)
# 准备好训练集的特征
devset = dataset.getDevSentences()
nDev = len(devset)
devFeatures = np.zeros((nDev, dimVectors))
devLabels = np.zeros((nDev,), dtype=np.int32)
for i in xrange(nDev):
words, devLabels[i] = devset[i]
devFeatures[i, :] = getSentenceFeature(tokens, wordVectors, words)
# 尝试不同的正则化系数
results = []
for regularization in REGULARIZATION:
random.seed(3141)
np.random.seed(59265)
weights = np.random.randn(dimVectors, 5)
print "Training for reg=%f" % regularization
# batch optimization
weights = sgd(lambda weights: softmax_wrapper(trainFeatures, trainLabels,
weights, regularization), weights, 3.0, 10000, PRINT_EVERY=100)
# 训练集上测效果
_, _, pred = softmaxRegression(trainFeatures, trainLabels, weights)
trainAccuracy = accuracy(trainLabels, pred)
print "Train accuracy (%%): %f" % trainAccuracy
# dev集合上看效果
_, _, pred = softmaxRegression(devFeatures, devLabels, weights)
devAccuracy = accuracy(devLabels, pred)
print "Dev accuracy (%%): %f" % devAccuracy
# 保存结果权重
results.append({
"reg" : regularization,
"weights" : weights,
"train" : trainAccuracy,
"dev" : devAccuracy})
# 输出准确率
print ""
print "=== Recap ==="
print "Reg\t\tTrain\t\tDev"
for result in results:
print "%E\t%f\t%f" % (
result["reg"],
result["train"],
result["dev"])
print ""
# 选最好的正则化系数
BEST_REGULARIZATION = None
BEST_WEIGHTS = None
best_dev = 0
for result in results:
if result["dev"] > best_dev:
best_dev = result["dev"]
BEST_REGULARIZATION = result["reg"]
BEST_WEIGHTS = result["weights"]
# Test your findings on the test set
testset = dataset.getTestSentences()
nTest = len(testset)
testFeatures = np.zeros((nTest, dimVectors))
testLabels = np.zeros((nTest,), dtype=np.int32)
for i in xrange(nTest):
words, testLabels[i] = testset[i]
testFeatures[i, :] = getSentenceFeature(tokens, wordVectors, words)
_, _, pred = softmaxRegression(testFeatures, testLabels, BEST_WEIGHTS)
print "Best regularization value: %E" % BEST_REGULARIZATION
print "Test accuracy (%%): %f" % accuracy(testLabels, pred)
# 画出正则化和准确率的关系
plt.plot(REGULARIZATION, [x["train"] for x in results])
plt.plot(REGULARIZATION, [x["dev"] for x in results])
plt.xscale('log')
plt.xlabel("regularization")
plt.ylabel("accuracy")
plt.legend(['train', 'dev'], loc='upper left')
plt.savefig("q4_reg_v_acc.png")
plt.show()(d)(4分)绘出在训练和开发过程中的分类准确率,并在x轴使用对数刻度来对正则化值进行相关设置。这应该自动化的进行。包括在你作业中详细展示的坐标图q4_reg_acc.png。简明解释最多三个句子在此坐标图中的显示情况。
解答: