【凸包性质】 POJ 1228 Grandpa's Estate
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 12470 | Accepted: 3496 |
Description
Input
Output
Sample Input
1 6 0 0 1 2 3 4 2 0 2 4 5 0
Sample Output
NO
Source
Tehran 2002 Preliminary
/*
暑假又到了_(・ω・」∠)_,诸位有没有感觉到智商被掏空呢?
“这次暑假集训结束后,我就去做那些没有危险的工作好了”说出了这样的flag的咱到底能不能正常过去呢OvO嘛现在武汉确实正在被水淹没不知所措的状态呢咱也开始感受到危机了就是=w=...
*/
这次看的题目是凸包,题意如下:
一个人拿到了他祖父的遗产——一个凸多边形的农场。原本地皮上用来划分地界用的那些绳子和一部分的钉子不知去向。那么是否能通过剩下的钉子来判断原本的土地呢?
首先,由题意可知,这张图是一个凸包。然后我们的任务是判断这个凸包是否能确定的表示一块土地,即:这些凸包上的点与任意一个凸包外的点,(在点全部使用的情况下)无法形成新的凸包。
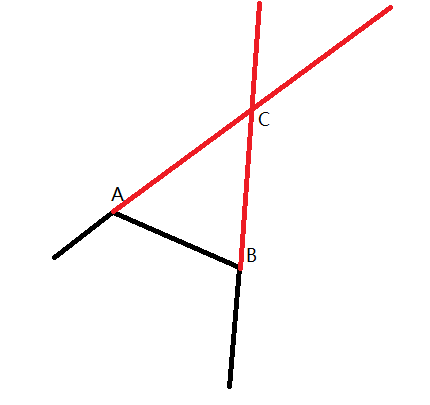
那么,我们假定有这么一条边AB。
因为所有的点都要作为凸包上的点,因此若要添加新点,则需要在不影响AB以及其他点的情况下添加。由凸包的性质可知在区域ABC内添加。必然满足条件。
那么,我们只要把这个区域给消除掉就好了。
因此可以得出结论:对于任意一条边,至少有一条临边与之共线。
那么接下来就好做了(好做了个鬼啦,明明一开始就猜到了做法却还是敲了几个小时)。
嘛,其实是一些细节需要注意,因为凸包的排序给的是所有的点按照逆时针+由近到远,而我们的排序在最后一条直线的地方是要由远到近所以在凸包排完之后把最后几个加进来就好了。。。除了起始和最后以外不可能存在共线所以没问题。
啊,最后如果只有2个点共线的情况原本应该是要特判的,然而出题人没考虑这样的数据吧?最开始没加也过了。。。不过严谨一点总没有错
题目地址:http://poj.org/problem?id=1228
题目代码:
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const double eps=1e-8;
int sgn(double x)
{
if(fabs(x)<eps) return 0;
if(x<0) return -1;
else return 1;
}
struct Point
{
double x,y;
Point() {}
Point(double _x,double _y)
{
x=_x;
y=_y;
}
Point operator -(const Point &b)const
{
return Point(x-b.x,y-b.y);
}
double operator ^(const Point &b)const
{
return x*b.y-y*b.x;
}
double operator *(const Point &b)const
{
return x*b.x+y*b.y;
}
};
double dist(Point a,Point b)
{
return sqrt((a-b)*(a-b));
}
const int MAXN=1005;
Point list[MAXN];
int Stack[MAXN],top;
int pr[MAXN];
void solve(int n)
{
for(int i=0;i<n;i++)
{
if(pr[i]==1 && pr[(i+1)%n]==1)
{
printf("NO\n");
return;
}
}
printf("YES\n");
return;
}
int judge(Point p1,Point p2)
{
//printf("(%.2f ,%.2f) (%.2f ,%.2f)\n",p1.x,p1.y,p2.x,p2.y);
double tmp=p1.x*p2.y-p2.x*p1.y;
//printf("tmp=%.2f\n",tmp);
if(fabs(tmp)<=eps) return 0;
else return 1;
}
bool _cmp(Point p1,Point p2)
{
double tmp=(p1-list[0])^(p2-list[0]);
if(sgn(tmp)>0)return true;
else if(sgn(tmp)==0 && sgn(dist(p1,list[0])-dist(p2,list[0]))<=0) return true;
else return false;
}
void Graham(int n)
{
Point p0;
int k=0;
p0=list[0];
for(int i=1; i<n; i++)
{
if((p0.y>list[i].y) || (p0.y==list[i].y && p0.x>list[i].x))
{
p0=list[i];
k=i;
}
}
swap(list[k],list[0]);
sort(list+1,list+n,_cmp);
top=2;
Stack[0]=0;
Stack[1]=1;
for(int i=2; i<n; i++)
{
int r=0;
while(top>1 && sgn((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]]))<0)
top--;
Stack[top++]=i;
}
int r=n-top;
int t=top-1;
for(int i=1;i<=r;i++)
{
Stack[top++]=Stack[t]-i;
}
//for(int i=0;i<n;i++) printf("%d\n",Stack[i]);
}
using namespace std;
int main()
{
int n;
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%lf%lf",&list[i].x,&list[i].y);
}
if(n<6)
{
printf("NO\n");
continue;
}
Graham(n);
int sum=0;
pr[n-1]=judge(list[Stack[0]]-list[Stack[n-1]],list[Stack[n-1]]-list[Stack[n-2]]);
pr[0]=judge(list[Stack[0]]-list[Stack[n-1]],list[Stack[1]]-list[Stack[0]]);
sum+=pr[n-1]+pr[0];
for(int i=1;i<n-1;i++)
{
pr[i]=judge(list[Stack[i]]-list[Stack[i-1]],list[Stack[i+1]]-list[Stack[i]]);
sum+=pr[i];
}
if(sum<3)
{
printf("NO\n");
continue;
}
solve(n);
}
return 0;
}