字符串匹配——KMP算法
字符串匹配——KMP算法
给定主串T和模式串P,返回P在T中首次出现的位置,如果P不存在于T中,返回-1。
这样的问题就是字符串匹配问题,这里给出KMP算法的思想。
设主串T的长度为n,模式串P的长度为m。
最大相同前缀后缀数组写法
先根据前缀后缀,求出前缀数组prefix,再通过前缀数组,快速迭代扫描主串,并找到首次匹配的位置,找不到则返回-1。
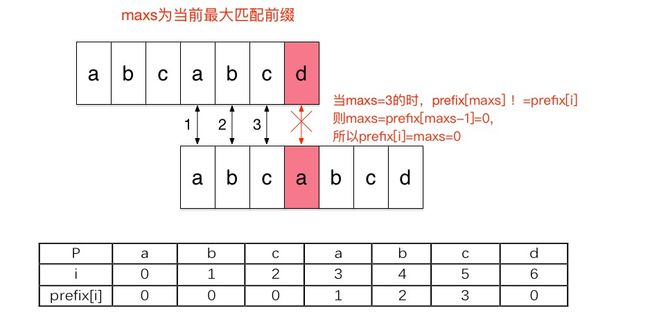
前缀数组prefix的求法
将prefix[0]初始化为0,设maxs为最大匹配前缀,m为模式串P的长度,设i为从1开始循环到m的迭代变量,当P[maxs]!=P[i]并且maxs>0时,循环执行maxs=prefix[maxs - 1],这一步的作用是找到除开i外的最大匹配前缀后缀,然后再判断加上i之后是否还能匹配,直到maxs为0或者匹配上为止。跳出循环后,再判断P[maxs]是否与P[i]相等,相等则maxs++,然后prefix[i]=maxs。通过这样的步骤就能求出next数组了。
伪代码
makePrefix(P)
01 initialize the array of prefix
02 m <- the length of P
04 maxs <- 0 // number of characters matched
05 for i <- 0 to m - 1 // scan the text from left to right
06 while maxs > 0 and P[maxs] ≠ P[i] do
07 maxs <- prefix[maxs - 1]
08 if P[maxs] = P[i] then maxs <- maxs + 1
10 prefix[i] <- maxs算法实现
const int maxNum = 1005;
int prefix[maxNum];
void markPrefix(const string &P) {
memset(prefix, 0, sizeof(prefix));
prefix[0] = 0;
int m = P.length();
// 最大前缀和后缀相等数目
int maxs = 0;
for(int i = 1; i < m; i++) {
// 在maxs>0并且
// P[maxs]和P[i]匹配失败的情况下
while(maxs > 0 && P[maxs] != P[i]) {
maxs = prefix[maxs - 1];
}
// 匹配+1
if(P[maxs] == P[i]) {
maxs++;
}
prefix[i] = maxs;
}
}基于最大相同前缀后缀的KMP算法
伪代码
KMP(T,P)
01 prefix <- Computer_prefix_Table(P)
02 n <- the length of T
03 m <- the length of P
04 maxs <- 0 // number of characters matched
05 for i <- 0 to n - 1 // scan the text from left to right
06 while maxs > 0 and P[maxs] ≠ T[i] do
07 maxs <- prefix[maxs - 1]
08 if P[maxs] = T[i] then maxs <- maxs + 1
10 if maxs = m then return i - m + 1
11 return -1算法实现
int KMP(const string &T, const string &P) {
// 产生prefix数组
markPrefix(P);
int n = T.length();
int m = P.length();
int maxs = 0;
for(int i = 0; i < n; i++) {
while(maxs > 0 && T[i] != P[maxs]) {
maxs = prefix[maxs - 1];
}
if(T[i] == P[maxs]) {
maxs++;
}
// 匹配成功
if(maxs == m) {
return i - maxs + 1;
}
}
return -1;
}测试主程序
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
const int maxNum = 1005;
int prefix[maxNum];
void markPrefix(const string &P) {
memset(prefix, 0, sizeof(prefix));
prefix[0] = 0;
int m = P.length();
// 最大前缀和后缀相等数目
int maxs = 0;
for(int i = 1; i < m; i++) {
// 在maxs>0并且
// P[maxs]和P[i]匹配失败的情况下
while(maxs > 0 && P[maxs] != P[i]) {
maxs = prefix[maxs - 1];
}
// 匹配+1
if(P[maxs] == P[i]) {
maxs++;
}
prefix[i] = maxs;
}
}
int KMP(const string &T, const string &P) {
// 产生prefix数组
markPrefix(P);
int n = T.length();
int m = P.length();
int maxs = 0;
for(int i = 0; i < n; i++) {
while(maxs > 0 && T[i] != P[maxs]) {
maxs = prefix[maxs - 1];
}
if(T[i] == P[maxs]) {
maxs++;
}
// 匹配成功
if(maxs == m) {
return i - maxs + 1;
}
}
return -1;
}
/** IN at the thought of though OUT 7 **/
int main() {
// 主串和模式串
string T, P;
while(true) {
// 获取一行
getline(cin, T);
getline(cin, P);
int res = KMP(T, P);
if(res == -1) {
cout << "主串和模式串不匹配。" << endl;
} else {
cout << "模式串在主串的位置为:" << res << endl;
}
}
return 0;
}输出数据
at the thought of
though
模式串在主串的位置为:7
afdasda
gdsfgdsf
主串和模式串不匹配。
gfdgaggdag
dag
模式串在主串的位置为:7
fgagakgl;sdakfgl;dskaflafdsfsd
;sda
模式串在主串的位置为:8
gagkagjkajgfklewiwfdafsaview
view
模式串在主串的位置为:24
asdfghjklqwertyuiop
p
模式串在主串的位置为:18next数组写法
next数组的求法
next数组可以通过将next[0]=-1,之后的元素则是最大相同前缀后缀数组prefix右移一位就能得到。
根据最大长度表求出了next 数组后,从而有1
失配时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值
而后,你会发现,无论是基于最大相同前缀后缀的匹配,还是基于next 数组的匹配,两者得出来的向右移动的位数是一样的。为什么呢?因为:
根据《最大相同前缀后缀》,失配时,模式串向右移动的位数 = 已经匹配的字符数 - 失配字符的上一位字符的最大长度值
而根据《next 数组》,失配时,模式串向右移动的位数 = 失配字符的位置 - 失配字符对应的next 值
- 其中,从0开始计数时,失配字符的位置 = 已经匹配的字符数(失配字符不计数),而失配字符对应的next 值 = 失配字符的上一位字符的最大长度值,两相比较,结果必然完全一致。
所以,你可以把《最大相同前缀后缀》看做是next 数组的雏形,甚至就把它当做next 数组也是可以的,区别不过是怎么用的问题。
伪代码
makeNext(P)
01 initialize the array of next
02 m <- the length of P
04 maxs <- 0 // number of characters matched
05 while i < m
06 while maxs > -1 and P[maxs] ≠ P[i] do
07 maxs <- next[maxs]
08 if maxs = -1 or P[maxs] = P[i] then
09 i <- i + 1
10 maxs <- maxs + 1
11 next[i] <- maxs算法实现
const int maxNum = 1005;
int next[maxNum];
void markNext(const string &P) {
memset(next, 0, sizeof(next));
next[0] = -1;
int m = P.length();
// 最大前缀和后缀相等数目
int maxs = 0;
for(int i = 1; i < m;) {
// 在maxs>-1并且
// P[maxs]和P[i]匹配失败的情况下
while(maxs > -1 && P[maxs] != P[i]) {
maxs = next[maxs];
}
// 匹配+1
if(maxs == -1 || P[maxs] == P[i]) {
i++;
maxs++;
}
next[i] = maxs;
}
}基于next数组的KMP算法
伪代码
KMP(T,P)
01 next <- Computer_next_Table(P)
02 n <- the length of T
03 m <- the length of P
04 maxs <- 0 // number of characters matched
05 for i <- 0 to n - 1 // scan the text from left to right
06 while maxs > -1 and P[maxs] ≠ T[i] do
07 maxs <- next[maxs]
08 if maxs = -1 or P[maxs] = T[i] then maxs <- maxs + 1
10 if maxs = m then return i - m + 1
11 return -1实现算法
int KMP(const string &T, const string &P) {
// 产生next数组
markNext(P);
int n = T.length();
int m = P.length();
int maxs = 0;
for(int i = 0; i < n; i++) {
while(maxs > -1 && T[i] != P[maxs]) {
maxs = next[maxs];
}
if(maxs == -1 || T[i] == P[maxs]) {
maxs++;
}
// 匹配成功
if(maxs == m) {
return i - maxs + 1;
}
}
return -1;
}主程序和输出数据
主程序和最大相同前缀后缀数组写法相差不大,将markNext和KMP函数进行替换就行了。数组数据是一致的,这里不在赘述。
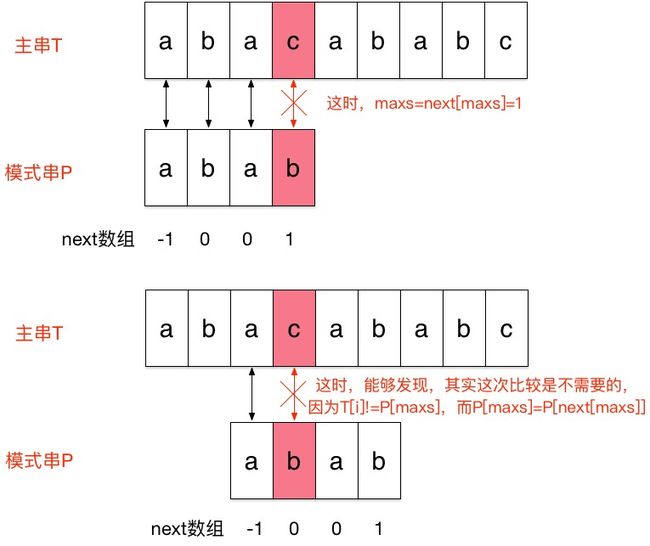
next数组的优化
通过上面两张图片,可以看出next数组的优化其实很简单,就是,模式串的P[maxs]不能等于P[next[maxs]]。因为如果相等的话,那么T[i]!=P[maxs]的情况,T[i]也是不等于P[next[maxs]]的。所以只需要将P[i]=maxs加上一个P[i]!=P[maxs]的条件就行了(为模式串当前遍历到的元素下标)。否则next[i]=next[maxs],这一步是递归的将下标从next[i]改为next[next[i]]。
至于为什么next[i]=maxs,这是因为next[i]存的是0->i-1的最长相同前缀后缀的值,而maxs本来就表示当前的最长相同前缀后缀的值。为什么不直接用next[i]=next[next[i]]呢,这是因为,next[i]的数值这时候并没有计算出来。
nextVal数组伪代码
makeNextVal(P)
01 initialize the array of nextVal
02 m <- the length of P
04 maxs <- 0 // number of characters matched
05 while i < m
06 while maxs > -1 and P[maxs] ≠ P[i] do
07 maxs <- nextVal[maxs]
08 if maxs = -1 or P[maxs] = P[i] then
09 i <- i + 1
10 maxs <- maxs + 1
11 if P[maxs] ≠ P[i] then
12 nextVal[i] <- maxs
13 else
14 nextVal[i] <- nextVal[maxs]算法实现
const int maxNum = 1005;
int nextVal[maxNum];
void markNextVal(const string &P) {
memset(nextVal, 0, sizeof(nextVal));
nextVal[0] = -1;
int m = P.length();
// 最大前缀和后缀相等数目
int maxs = 0;
for(int i = 1; i < m;) {
// 在maxs>-1并且
// P[maxs]和P[i]匹配失败的情况下
while(maxs > -1 && P[maxs] != P[i]) {
maxs = nextVal[maxs];
}
// 匹配+1
if(maxs == -1 || P[maxs] == P[i]) {
i++;
maxs++;
}
// 注意刚刚比较的是i-1,然后i++,maxs++
// 如果两者不等,则按markNext算法的操作
// 因为不能出现p[maxs]==p[next[maxs]],则递归next[i]=next[maxs]
if(P[maxs] != P[i]) {
nextVal[i] = maxs;
} else {
nextVal[i] = nextVal[maxs];
}
}
}算法分析
无论是最大相同前缀后缀prefix还是next数组的解法,其时间复杂度都是一样的,这里给出next写法的分析。2
假设现在文本串T匹配到 i 位置,模式串P匹配到 j 位置
- 如果j = -1,或者当前字符匹配成功(即T[i] == P[j]),都令i++,j++,继续匹配下一个字符;
- 如果j != -1,且当前字符匹配失败(即T[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
我们发现如果某个字符匹配成功,模式串首字符的位置保持不动,仅仅是i++、j++;如果匹配失配,i 不变(即 i 不回溯),模式串会跳过匹配过的next [j-1]个字符。整个算法最坏的情况是,当模式串首字符位于i - j的位置时才匹配成功,算法结束。
所以,如果文本串的长度为n,模式串的长度为m,那么匹配过程的时间复杂度为O(n),算上计算next的O(m)时间,KMP的整体时间复杂度为O(m + n)。
- 参考July的从头到尾彻底理解KMP(2014年8月22日版) 根据《最大长度表》求next 数组 ↩
- 参考July的 从头到尾彻底理解KMP(2014年8月22日版)KMP的时间复杂度分析 ↩