快速排序的相关算法题(java)
快速排序的相关算法题(java)
标签(空格分隔): 排序 java 快排 算法
关于二分查找的,可以参考我的这篇博客二分查找的相关算法题
关于归并排序的的,可以参考我的这篇博客归并排序 递归版和非递归版的实现(java)
转载请注明原博客地址:
源码下载地址:
最近在做各个大公司的笔试题 ,比如阿里,腾讯,cvte等等,经常会遇到关于快速排序的各种算法题,包括时间复杂度,空间复杂度的分析与计算等等,于是本人查阅了相关的资料,先总结如下
本篇博客主要讲解一下三点
- 快排是怎样实现的?
- 怎样用最快的速度找出数组中出现次数超过一半的数字
- 要求找出数组中最小的第k个数,时间复杂度最低
快排是怎样实现的?
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j–),找到第一个小于key的值A[j],将A[j]和A[i]互换;
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]互换;
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
举例说明
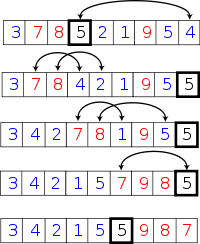
举例来说,现有数组 arr = [3,7,8,5,2,1,9,5,4],分区可以分解成以下步骤:
首先选定一个基准元素,这里我们元素 5 为基准元素(基准元素可以任意选择):
首先选定一个基准元素,这里我们元素 5 为基准元素(基准元素可以任意选择):
pivot
↓
3 7 8 5 2 1 9 5 4将基准元素与数组中最后一个元素交换位置,如果选择最后一个元素为基准元素可以省略该步:
pivot
↓
3 7 8 4 2 1 9 5 5从左到右(除了最后的基准元素),循环移动小于基准元素 5 的所有元素到数组开头,留下大于等于基准元素的元素接在后面。在这个过程它也为基准元素找寻最后摆放的位置。循环流程如下:
循环 i == 0 时,storeIndex == 0,找到一个小于基准元素的元素 3,那么将其与 storeIndex 所在位置的元素交换位置,这里是 3 自身,交换后将 storeIndex 自增 1,storeIndex == 1:
pivot
↓
3 7 8 4 2 1 9 5 5
↑
storeIndex循环 i == 3 时,storeIndex == 1,找到一个小于基准元素的元素 4:
┌────┐ pivot
↓ ↓ ↓
3 7 8 4 2 1 9 5 5
↑ ↑
storeIndex i交换位置后,storeIndex 自增 1,storeIndex == 2:
pivot
↓
3 4 8 7 2 1 9 5 5
↑
storeIndex循环 i == 4 时,storeIndex == 2,找到一个小于基准元素的元素 2:
┌───-┐ pivot
↓ ↓ ↓
3 4 8 7 2 1 9 5 5
↑ ↑
storeIndex i交换位置后,storeIndex 自增 1,storeIndex == 3:
pivot
↓
3 4 2 7 8 1 9 5 5
↑
storeIndex循环 i == 5 时,storeIndex == 3,找到一个小于基准元素的元素 1:
┌────┐ pivot
↓ ↓ ↓
3 4 2 7 8 1 9 5 5
↑ ↑
storeIndex i交换后位置后,storeIndex 自增 1,storeIndex == 4:
pivot
↓
3 4 2 1 8 7 9 5 5
↑
storeIndex循环 i == 7 时,storeIndex == 4,找到一个小于等于基准元素的元素 5:
┌──────┐ pivot
↓ ↓ ↓
3 4 2 1 8 7 9 5 5
↑ ↑
storeIndex i交换后位置后,storeIndex 自增 1,storeIndex == 5:
pivot
↓
3 4 2 1 5 7 9 8 5
↑
storeIndex循环结束后交换基准元素和 storeIndex 位置的元素的位置:
pivot
↓
3 4 2 1 5 5 9 8 7
↑
storeIndex那么 storeIndex 的值就是基准元素的最终位置,这样整个分区过程就完成了。
下面我们来看一下源码是怎样实现的
1. 简单来说就是先找出一个索引,左边的数都比他小,右边的数都比他大 ,接着利用递归排列左边和右边的数,直到low>=high
private static void qSort(int[] data, int low, int high) {
int pivot;
if (low < high) {
pivot = partition(data, low, high);
qSort(data, 0, pivot - 1);
qSort(data, pivot + 1, high);
}
}
2. 下面我们来看一下partition函数式怎样实现的
private static int partition(int[] data, int low, int high) {
int pivotKey;
pivotKey = data[low];
while (low < high) {
// 将小于基准点的值得数放到前面
while (low < high && data[high] >= pivotKey) {//
high--;
}
ArrayUtils.exchangeElements(data, low, high);
// 将大于基准点的值得数放到后面
while (low < high && data[low] <= pivotKey) {
low++;
}
ArrayUtils.exchangeElements(data, low, high);
}
// 返回基准点的索引
return low;
}
其实就是从两端进行扫描,发现小于基准点的 数的时候,将其放到前面到,发现大于基准点的数的时候,将其发到后面去
到此快速排序的分析为止
数组中出现次数超过一半的数字
一、问题描述
给定一个数组,数组中的数据无序,在一个数组中找出其第k个最小的数,例如对于数组x,x = {3,2,1,4,5,6},则其第2个最小的数为2。
二、解题思路
本算法跟快排的思想相似,首先在数组中选取一个数centre作为枢纽,将比centre小的数,放到centre的前面将比centre大的数,放到centre的后面。如果此时centre的位置刚好为k,则centre为第k个最小的数;如果此时centre的位置比k前,则第k个最小数一定在centre后面,递归地在其右边寻找;如果此时centre的位置比k后,则第k个最小数一定在centre后面,递归地在其左边寻找。
三、代码
package com.xujun.quicksort;
import java.util.Collections;
public class MinIndex {
static int[] a = new int[] { 20, 9, 3, 5, 26, 100, 8, -1, 7, 50, -5, 20, -1 };
public static void main(String[] args) {
System.out.println("before sort");
ArrayUtils.printArray(a);
int k=8;
int pivot = findMinIndexInArray(a, k);
System.out.println("after sort");
ArrayUtils.printArray(a);
System.out.println("数组中最小的第"+k+"个数是 " + a[pivot]);
}
private static int findMinIndexInArray(int[] data, int k) {
if (data == null || data.length < k) {
return -1;
}
int start = 0;
int end = data.length - 1;
int pivot = partition(data, start, end);
while (pivot != k - 1) {
if (pivot < k - 1) {
start = pivot + 1;
pivot = partition(data, start, end);
} else {
end = pivot - 1;
pivot = partition(data, start, end);
}
}
return pivot;
}
private static int partition(int[] data, int low, int high) {
int pivotKey;
/* * pivotKey = data[low];// 选取low作为基准点,pivotKey为基准点的值 */
int middle = low + (high - low) / 2;
if (data[low] > data[high]) {// 较大的数存在high中
ArrayUtils.exchangeElements(data, low, high);
}
if (data[middle] > data[high]) {
ArrayUtils.exchangeElements(data, middle, high);
}
if (data[middle] > data[low]) {
ArrayUtils.exchangeElements(data, middle, low);
}
pivotKey = data[low];// 选取low作为基准点,pivotKey为基准点的值
// 将大于基准点的值得数放到后面
while (low < high) {
while (low < high && data[high] >= pivotKey) {//
high--;
}
data[low] = data[high];
// 将小于基准点的值得数放到前面
while (low < high && data[low] <= pivotKey) {
low++;
}
data[high] = data[low];
}
data[low] = pivotKey;
// 返回基准点的索引
return low;
}
}2 数组中最小的第k个数
一、问题描述
给定一个数组,找出数组中元素出现次数超过数组长度一半的元素
如数组:
[4, 3, 2, 1, 1, 1, 1, 1, 1, 0 ]
其中超过一半的元素就是 1
二、解题思路
1)本题同样可以医用快速排序的思想来做,如果一个数字出现次数超过一般,那么排好序的数组的中间数肯定就是出现次数超过一半的数字
2)考虑异常情况下,出现次数没有超过一半
遍历数组,检查一下
三、代码
package com.xujun.quicksort;
import java.util.Collections;
public class MoreThanHalf {
static int[] a = new int[] { 20, 9, 3, 5, 10,10,10,10,10 };
public static void main(String[] args) {
System.out.println("before sort");
ArrayUtils.printArray(a);
int k = 8;
int pivot = findMoreHalfInArray(a);
int target = a[pivot];
boolean checkIsMoreThanHalf = checkIsMoreThanHalf(a, target);
if(checkIsMoreThanHalf){
System.out.println("after sort");
ArrayUtils.printArray(a);
System.out.println("超过一般的数是="+target);
}else{
System.out.println("没有超过一般的数字");
}
}
private static boolean checkIsMoreThanHalf(int[] data, int target) {
int half=data.length/2;
int count=0;
for(int i=0;i<data.length;i++){
if(data[i]==target){
count++;
}
}
return count>=half?true:false;
}
private static int findMoreHalfInArray(int[] data) {
if (data == null || data.length <= 0) {
return -1;
}
int start = 0;
int end = data.length - 1;
int half = data.length / 2;
int pivot = partition(data, start, end);
while (pivot != half - 1) {
if (pivot < half - 1) {// 枢轴在一半的 左边
start = pivot + 1;
pivot = partition(data, start, end);
} else {// 枢轴在一半(中间点)的右边
end = half - 1;
pivot = partition(data, start, end);
}
}
return pivot;
}
private static int partition(int[] data, int low, int high) {
int pivotKey;
/* * pivotKey = data[low];// 选取low作为基准点,pivotKey为基准点的值 */
int middle = low + (high - low) / 2;
if (data[low] > data[high]) {// 较大的数存在high中
ArrayUtils.exchangeElements(data, low, high);
}
if (data[middle] > data[high]) {
ArrayUtils.exchangeElements(data, middle, high);
}
if (data[middle] > data[low]) {
ArrayUtils.exchangeElements(data, middle, low);
}
pivotKey = data[low];// 选取low作为基准点,pivotKey为基准点的值
// 将大于基准点的值得数放到后面
while (low < high) {
while (low < high && data[high] >= pivotKey) {//
high--;
}
data[low] = data[high];
// 将小于基准点的值得数放到前面
while (low < high && data[low] <= pivotKey) {
low++;
}
data[high] = data[low];
}
data[low] = pivotKey;
// 返回基准点的索引
return low;
}
}
关于二分查找的,可以参考我的这篇博客二分查找的相关算法题
关于归并排序的的,可以参考我的这篇博客归并排序 递归版和非递归版的实现(java)
转载请注明原博客地址:
源码下载地址: