hdu 5434 Peace small elephant
题目链接
此题是BestCoder Round #55 中的一个题
Problem Description
Xiao Ming likes playing the international chess ,especially like the elephant(it can move by slant while no barrier),
but he think the big elephant of the chess is cruel,and a kind of small elephant is not as cruel as the big elephant.
Its attack range is checks on the ramp of the small elephant's check's right angle.Now Ming is going to put many small elephants on his chessboard.
It's interesting that when two small elephants have a common side they'll become one solidarity elephant,
and more than 2 small elephants also can do this if satisfy the condition,and the attack range of solidarity elephants is same as the small elephant.
Now there is a requirement that it's empty on anyone of elephants' attack range(no piece).Xiao Ming has a special chessboard with m∗n checks.
Please figure out the number of all the plans that satisfy the condition.As the number is too big,we need to have a modulo 1000000007 .
The following is pictures show the attack range of elephants with different shape,"X"means attack range.
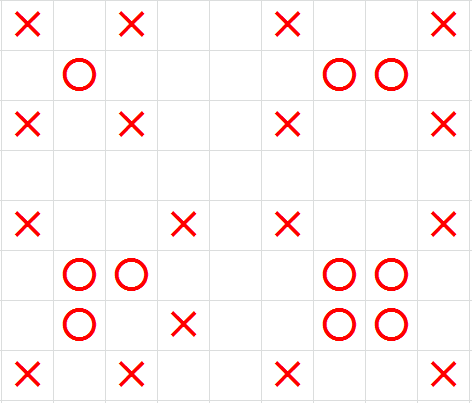
but he think the big elephant of the chess is cruel,and a kind of small elephant is not as cruel as the big elephant.
Its attack range is checks on the ramp of the small elephant's check's right angle.Now Ming is going to put many small elephants on his chessboard.
It's interesting that when two small elephants have a common side they'll become one solidarity elephant,
and more than 2 small elephants also can do this if satisfy the condition,and the attack range of solidarity elephants is same as the small elephant.
Now there is a requirement that it's empty on anyone of elephants' attack range(no piece).Xiao Ming has a special chessboard with m∗n checks.
Please figure out the number of all the plans that satisfy the condition.As the number is too big,we need to have a modulo 1000000007 .
The following is pictures show the attack range of elephants with different shape,"X"means attack range.

Input
There are at most
5 testcases .
For each testcase contains two integers n,m ,meaning as in the title.
1≤n≤1000000000,1≤m≤7
For each testcase contains two integers n,m ,meaning as in the title.
1≤n≤1000000000,1≤m≤7
Output
For each testcase print a single integer - the number of all the plans that satisfy the condition.
Sample Input
1 1 2 3
Sample Output
2 50
Source
BestCoder Round #55 ($)
题意:看图就可以知道,一个象的左上右上,左下,右下不能放象,但是合体象不一样,看图即可明白!
分析(借用BC官方题解说明):
这个题用状态转移得到矩阵,再矩阵快速幂就可以了。
合体象的攻击范围是变少了的,我们可以理解为,一个小象会对自身的四个正方向产生保护,可以得到结论,只要附近有小象,我们就可以放。
可以枚举i行的所有状态和i−1行的所有状态,判断是否可以转移。
将状态转移方程改为矩阵,最后矩阵快速幂就可以了。
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define mod 1000000007
#define ll long long
using namespace std;
ll p[128][128];
ll N,n,m;
bool isok(int x,int k)
{
if(x&(1<<k)) return true;
return false;
}
void init()
{
memset(p,0,sizeof(p));
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
int ok=1;
for(int k=0;k<m;k++)
{
if(isok(j,k))
{
if((k<m-1)&&isok(i,k+1)&&!isok(i,k)&&!isok(j,k+1))
{
ok=0;
break;
}
if(k>0&&isok(i,k-1)&&!isok(i,k)&&!isok(j,k-1))
{
ok=0;
break;
}
}
}
if(ok) p[i][j]=1;
}
}
}
struct node
{
ll dp[128][128];
};
node multi(node a,node b)
{
node tem;
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
tem.dp[i][j]=0;
for(int k=0;k<N;k++)
{
tem.dp[i][j]+=a.dp[i][k]*b.dp[k][j];
tem.dp[i][j]%=mod;
}
}
}
return tem;
}
node get(ll num)
{
node res,a;
memcpy(a.dp,p,sizeof(a.dp));
memset(res.dp,0,sizeof(res.dp));
for(int i=0;i<N;i++)
res.dp[i][i]=1;
while(num)
{
if(num&1) res=multi(res,a);
num>>=1;
a=multi(a,a);
}
return res;
}
int main()
{
while(scanf("%lld%lld",&n,&m)!=EOF)
{
N=1<<m;
init();
node res=get(n-1);
ll ans=0;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ans=(ans+res.dp[i][j])%mod;
printf("%lld\n",ans);
}
return 0;
}