EM算法学习笔记2：深入理解

文章《EM算法学习笔记1：简介》中介绍了EM算法的主要思路和流程，我们知道EM算法通过迭代的方法，最后得到最大似然问题的一个局部最优解。本文介绍标准EM算法背后的原理。

我们有样本集X，隐变量Z，模型参数 θ ，注意他们3个都是向量，要求解的log似然函数是 lnp(X|θ) ，而这个log似然函数难以求解，我们假设隐变量Z已知，发现 lnp(X,Z|θ) 的最大似然容易求解。

有一天，人们发现引入任意一个关于隐变量的分布q(Z)，对于这个log似然函数，存在这样一个分解：

lnp(X|θ)=L(q,θ)+KL(q||p).(1)

其中：

L(q,θ)=∑Zq(Z)lnp(X,Z|θ)q(Z).(2)

KL(q||p)=−∑Zq(Z)lnp(Z|X,θ)q(Z).(3)

L(q,θ) is a functional of q(Z), and a function of θ .
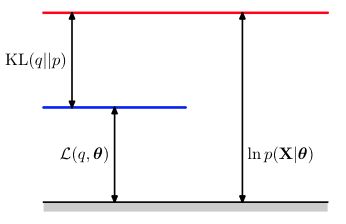
因为KL距离是大于等于0的，当且仅当 q(Z)=p(Z|X,θ) 时等于0，所以 L(q,θ) 是log似然函数 lnp(X|θ) 的一个lower bound，也就是如下图的关系：

要证明(1)式成立，将如下的(4)式代入(2)中，再把(2),(3)代入(1)式右边，整理后可以看到(1)式两边相等。

lnp(X,Z|θ)=lnp(Z|X,θ)+$lnp(X|θ).(4)

假设当前初始化了一个 θold 。
在E step，我们固定 θold ，根据q(Z)来最大化lower bound L(q,θold) 。我们直接令 q(Z)=p(Z|X,θold) ，使L达到最大，而 lnp(X|θ) 不依赖于q(Z)，所以它的值不变。

此时在对(2)式把q(Z)用 p(Z|X,θold) 替换掉，可以得到：

L(q,θ)=∑Zp(Z|X,θold)lnp(X,Z|θ)−∑Zp(Z|X,θold)lnp(Z|X,θold)=E(θ,θold)+const.(5)

这个 E(θ,θold) 就是(5)中第一个求和式：在假设隐变量Z已知时的log似然函数，关于隐变量Z的后验概率的期望。
const是包含了减号及减号后面的内容，在我们固定 θold 的情况下，是个固定值。
所以在E step这一步，我们需要计算出期望 E(θ,θold) ，下一步的最大化L也就可以转化成最大化这个期望，而期望中包含的lnp(X,Z|\theta)，最好能是连乘或指数形式，这样下一步最大似然的计算会简单很多。
也就是说，我们绕开了对 lnp(X|θ) 直接求最大似然。

在M step，我们固定q(Z)，根据 θ 来最大化lower bound L(q,θold) （实质上也是最大化期望E），并得到一个令L最大的 θnew ，此时L达到最大，且 lnp(X|θ) 也相应增大。
而此时KL距离又变大了，q也已经不是最优了，所以要再回到E step。

如此反复迭代，lnp(X|theta)总是在增大的，等到它不再增大，或者增大速度很慢很慢时，我们可以认为达到了局部最优。

上述EM算法的过程可以用下图直观地解释。

红色线是我们要最大化的log似然函数 lnp(X|θ) ，开始时先设定一个 θold 。
在E step估计隐变量Z的后验概率，得到一个 L(q,θold) ，如蓝色线所示。
在M step来最大化 L(q,θold) ，得到绿色线，此时它更好地接近 lnp(X|θ) ，我们得到一个 θnew 。

这个EM算法的理解是来自《Pattern Recognition And Machine Learning》中的”EM algorithm in general”，其中在引入q(Z)时已经涉及到了变分的思想，本文的EM内容有助于理解LDA的原始论文中的EM算法求解参数的部分。

[email protected]
发现一个讲em思想讲的很好的博客，仰慕~
http://blog.csdn.net/zouxy09/article/details/8537620