计算机图形学（二）输出图元_20_章节总结_程序展示_蜗形线、心形线、螺旋线

    蜗形线、心形线、螺旋线  

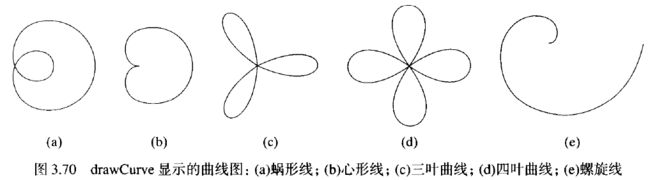
       最后一个程序显示了圆公式的某些变化，其中使用了参数极坐标方程(3.28)来计算曲线路径的点。这些点用做显示弧的逼近折线中直线段的端点。图3.70中的弧通过圆半径r的变化来生成。按照r的不同变化，可生成蜗形线、心形线、螺旋线或其他类似的图形。

#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>


#include <iostream.h>
struct screenPt
{
    GLint x;
	GLint y;


};
typedef enum {limacon = 1, cardioid, threeLeaf, fourLeaf, spiral} curveName;
GLsizei winWidth = 600, winHeight = 500;  //Initial display window size.


void init (void)
{
    glClearColor (1.0, 1.0, 1.0, 1.0);
	glMatrixMode (GL_PROJECTION);
	gluOrtho2D (0.0, 200.0, 0.0, 150.0);
}


void lineSegment (screenPt pt1, screenPt pt2)
{
    glBegin (GL_LINES);
	    glVertex2i (pt1.x, pt1.y);
		glVertex2i (pt2.x, pt2.y);
	glEnd ( );
}


void drawCurve (GLint curveName)
{
    /* The limacon of Pascal is a modification of the circle equation
	 * with the radius varying as r = a * cos (theta) + b, where a 
	 * and b are constants. A cardioid is a limacon with a = b.
	 * Three-leaf and four-leaf curves are generated when
	 * r = a * cos (n * theta), with n = 3 and n = 2, respectively.
	 * A spiral is displayed when r is a multiple of theta.
	 */
	 
	const GLdouble twoPi = 6.283185;
	const GLint a = 175, b = 60;
	GLfloat r, theta, dtheta = 1.0 / float (a);
	GLint x0 = 200; y0 = 250;     // Set an initial screen position.
	screenPt curvePt[2];
	glColor3f (0.0, 0.0, 0.0);    // Set curve position.
	curvePt[0].x = x0;          // Initialize curve position.
	curvePt[0].y = y0;


    switch (curveName){
	    case limacon: curvePt[0].x += a + b; break;
		case cardioid: curvePt[0].x += a + a; break;
		case threeLeaf: curvePt[0].x += a;   break;
		case fourLeaf: curvePt[0].x += a;    break;
		case spiral:   break;
		default:       break;
	}	
	
	theta = dtheta;
	while (theta < two_Pi){
	    switch (curveName){
		    case limacon:
			    r = a * cos (theta) + b;     break;
			case cardioid:
			    r = a * (1 + cos (theta));   break;
			case threeLeaf:
			    r = a * cos (3 * theta);     break;
			case fourLeaf:
				r = a * cos (2 * theta);     break;
			case spiral: 
			    r = (a / 4.0) * theta;       break;
			default:                         break;
		}
		
		curvePt[1].x = x0 + r * cos (theta);
		curvePt[1].y = y0 + r * sin (theta);
		lineSegment (curvePt[0], curvePt[1]);
		
		curvePt[0].x = curvePt[1].x;
		curvePt[0].y = curvePt[1].y;
		theta += dtheta;
	}
}


void displayFcn (void)
{
    GLint curveNum;
	glClear (GL_COLOR_BUFFER_BIT);     // Clear display window.
	cout << "\nEnter the integer value corresponding to\n";
	cout << "one of the following curve names.\n";
	cont << "Press any other key to exit.\n";
	cout << "\n1-limacon, 2-cardioid, 3-threeLeaf, 4-fourLeaf, 5-spiral: ";
	cin >> curveNum;
	
	if (curveNum == 1 || curveNum == 2 || curveNum == 3 || curveNum == 4 || curveNum == 5)
	    drawCurve (curveNum);
	else
	    exit (0);
	glFlush ( );
}


void winReshpeFcn (GLint newWidth, GLint newHeight)
{
    glMatrixMode (GL_PROJECTION);
	glLoadIdetity ( );
	gluOrtho2D (0.0, (GLdouble) newWidth, 0.0, (GLdouble) newHeight);
	glClear (GL_COLOR_BUFFER_BIT);
}


void main (int argc, char** argv)
{
    glutInit (&argc, argv);
	glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition (100, 100);
	glutInitWindowSize (winWidth, winHeight);
	glutCreateWindow ("Draw Curves");
	init ( );
	glutDisplayFunc(displayFcn);
	glutReshapeFunc(winReshpeFcn);
	glutMainLoop ( );

}