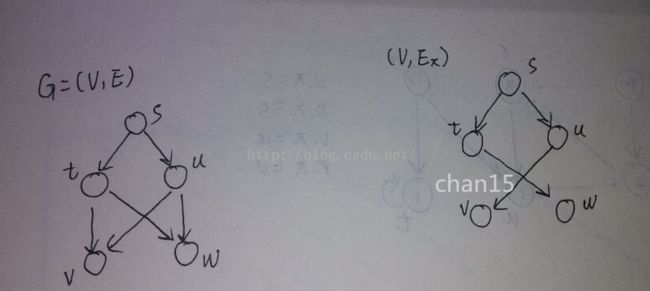算法导论22.2广度优先搜索 练习总结
22.2-1 请计算出在有向图 22-2(a) 上运行广度优先搜索算法后的 d 值和 π 值,这里假定结点 3 为算法所用的源结点。
ANSWER:
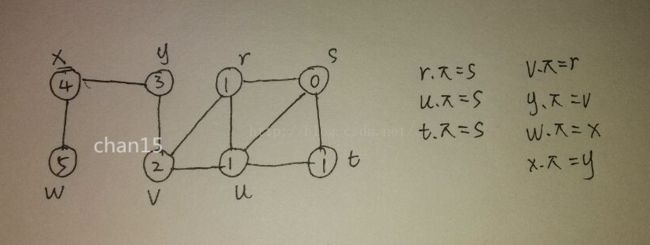
22.2-2 请计算出在图 22-3 所示无向图上运行广度优先搜索算法后的 d 值和 π 值。这里假定结点 u 为算法所用的源结点。
22.2-3 证明:使用单个位来存放每个结点的颜色即可。这个论点可以通过证明将算法第 18 行的伪代码删除后,BFS 过程生成的结果不变来得到。
ANSWER:证明:在 BFS 伪代码中,并没有对结点判断是否为黑色,所以删除第 18 行将结点着黑色并不会对结果有影响。对结点着黑色只是易于观察已计算距离的结点,事实上队列 Q 已记录待计算距离的结点。
22.2-4 如果将输入的图用邻接矩阵来表示,并修改算法来应对此种形式的输入,请问 BFS 的运行时间将是多少?
ANSWER:BFS 需要遍历图的所有边,利用邻接矩阵遍历所有边需要 O( V^2 ) 时间。
22.2-5 证明:在广度优先搜索算法里,赋给结点 u 的 u.d 值与结点在邻接链表里出现的次序无关。使用图 22-3 作为例子,证明:BFS 所计算出的广度优先树可以印邻接链表中的次序不同而不同。
ANSWER:① u.d = δ(s, u),而结点 s 到结点 u 的最短路径只与结点之间的链接有关,与结点爱邻接链表中出现的次序无关。
22.2-6 举出一个有向图 G = (V, E) 的例子,对于源结点 s ∈ V 和一组树边 Eπ ∈ E,使得对于每个结点 v ∈ V,图(V, Eπ) 中从源结点 s 到结点 v 的唯一简单路径也是图 G 中的一条最短路径,但是,不管邻接链表里结点之间的次序如何,边集 Eπ 都不能通过在图 G 上运行 BFS 来得到。
22.2-7 职业摔跤手可以分为两种各类型:“娃娃脸”(“好人”)型和“高跟鞋”(“坏人”)型。在任意一堆职业摔跤手之间都有可能存在竞争关系。假定有 n 个职业摔跤手,并且有一个给出竞争关系的 r 对摔跤手的链表。请给出一个时间为 O( n+r ) 的算法来判断是否可以将某些摔跤手划分为“娃娃脸”型,而剩下的划分为“高跟鞋”型,使得所有的竞争关系均只存在于娃娃脸型和高跟鞋型选手之间。如果可以进行这种划分,则算法还应当生成一种这样的划分。
ANSWER:相当于划分成二分图。
给每个结点增加一个属性,定为 good(好人)或者 bad(坏人)。
链表中的结点的属性必与该链表头结点属性相反。按照这个规则遍历每个链表,第一个链表表头结点属性设为 good,若在遍历过程,发现新定义的属性与先前定义的属性冲突,则不可以划分;反之,则可以划分,并且属性为 good 和 bad 的结点就是相应的两类。
*22.2-8 我们将一棵树 T = (V, E) 的直径定义为 max (u, v∈V) δ(u, v),也就是说,树中所有最短路径距离的最大值即为树的直径。请给出一个有效算法来计算树的直径,并分析算法的运行时间。
ANSWER:根据树的直径的性质:树的直径的路径的两个端点之一必定是以任一结点为源结点的最大路径的末结点。所以运行两次 BFS 搜索,第一次随机选择一个结点作为源结点;第二次选择第一次搜索结果中路径最大值的结点作为源结点,第二次 BFS 搜索得出的最大路径即为树的直径。时间复杂度为O(V+E)。