初学伸展树区间建树(A Simple Problem with Integers)
一.几个重要概念
1.伸展树属于一种平衡树,也是一棵普通的二叉排序树。
2.伸展树的核心在于它的伸展(splay)操作,对于每一次的伸展操作(把某个节点放到目标节点的下面),都有可能改变树中每个节点的分布,从而改变整个树的形状。
3.伸展树对于树的平横性没有要求,与平衡树不同,任意两个节点都可以有任意的深度差,不需要记录平衡树的冗余信息。
4.伸展树每次搜索的复杂度平摊下来都是log(n),如果遇到插入的数每次都是两个极端的情况,此时伸展树退化为链状,复杂度最坏。
5.伸展树的旋转操作
伸展树中的旋转操作不同于平衡树,一般对于这个操作最基本的方法就是一层一层的向上旋转,无法改变树的形态,而伸展树中不需要
控制树的形态,从而有新的方法来进行旋转。
在伸展树的旋转操作一共可以分为三类(按形状分),每类都有镜像。
1 )单旋转:当前节点的父节点即为目标节点,那么直接左旋或者右旋即可。
goal x
/ -> \
x goal
2)一字型:顾名思义树枝的形状呈现为一字型,如图
z x
/ y \
y -> / \ -> y
/ x z \
x z
此时先对y进行旋转,再对x进行旋转
3)之字形:顾名思义树枝的形状呈现为之字形,如图
z z
/ / x
y -> x -> / \
\ / y z
x y
此时先对x旋转,之后再对x进行一次旋转
以上的旋转左旋还是右旋辨别有一个小窍门,对于x来说,如果是y的左节点,那么右旋,如果是y的右节点,那么左旋,
一字型的两次旋转方向相同,之字形相反。
-------------------------------------以上是基础必备知识------------------------------------------
那么我们如何像线段树一样运用伸展树对数列的区间经行操作呢?
先来看一道题目
A Simple Problem with Integers
Description
给出了一个序列,你需要处理如下两种询问。
"C a b c"表示给[a, b]区间中的值全部增加c (-10000≤ c ≤ 10000)。
"Q a b" 询问[a, b]区间中所有值的和。
Input
第一行包含两个整数N,Q。1≤ N,Q ≤ 100000.
第二行包含n个整数,表示初始的序列A (-1000000000≤ Ai ≤1000000000)。
接下来Q行询问,格式如题目描述。
Output
对于每一个Q开头的询问,你需要输出相应的答案,每个答案一行。
Sample Input
10 5 1 2 3 4 5 6 7 8 9 10 Q 4 4 Q 1 10 Q 2 4 C 3 6 3 Q 2 4
Sample Output
4 55 9 15
题意很明确,就是给出更新操作和查询操作让我们来执行,用线段树来写很方便,效率很高,但是如果用伸展树该如何解决。
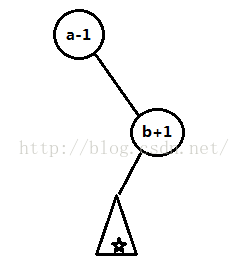
首先我们知道伸展树的中序序列就是我们要维护的区间,那么我们假设现在要维护的区间为[a,b],那么如果a-1号节点的右儿子刚好是b+1,那么此时我们的区间就刚好是
b+1号节点的左儿子?如图
为了防止b+1不能直接转移到a-1的右儿子上,我们直接把a-1放到根节点上,继而b+1号节点就能顺理成章的转移到a-1的右节点上
这样以来区间就能确定了,但是由于a-1和b+1都有有可能越界,我们需要另外虚设两个节点防止越界,上代码:
#define keytree ch[ch[root][1]][0]
void newnode(int &x,int p,int v)
{
x=++top;//为每个节点分配编号
ch[x][0]=ch[x][1]=0;//每个节点末端初始化为终端节点
pre[x]=p;
val[x]=v;
add[x]=0;
sum[x]=v;
siz[x]=1;
}
void init(int n)
{
for(int i=0; i<n; i++) scanf("%d",&tmp[i]);
root=top=0;
siz[0]=ch[0][0]=ch[0][1]=add[0]=sum[0]=pre[0]=0;//0为终端节点
newnode(root,0,-1);//虚设节点
newnode(ch[root][1],root,-1);//虚设节点
build(keytree,0,n-1,ch[root][1]);
pushup(ch[root][1]);
pushup(root);
}
两个虚设的节点在整个数列的两端维护整个数列
对于0-n-1个结点来说,为了从一开始就尽可能减少复杂度,我们从中间节点开始建树,如代码:
void build(int &x,int l,int r,int p)
{
int mid=(l+r)>>1;
newnode(x,p,tmp[mid]);
if(l<mid) build(ch[x][0],l,mid-1,x);
if(r>mid) build(ch[x][1],mid+1,r,x);
pushup(x);
}
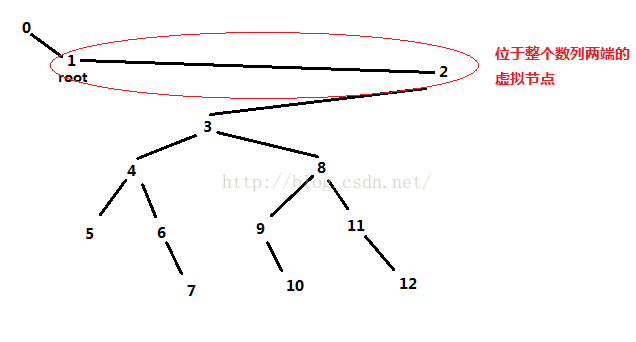
那么样例中的树建好后应该是这样
图中的数字代表的是节点的编号,而不是原数列中的下标,不要被迷惑了。
每次的区间就被安排在了keytree那个位置
对于图中的的每一个节点来说,他在序列中对应的编号就是它的左树节点个数+1,在找第原序列中的第几号时按照的就是这个规律。
题目源代码:
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define maxn 100020
#define keytree ch[ch[root][1]][0] ///keytree代表splay之后的区间节点
int ch[maxn][2],pre[maxn],tmp[maxn],val[maxn],siz[maxn],add[maxn];
///ch用来存储节点的左孩子右孩子,add为延迟标记,siz代表子树中有多少个节点
long long sum[maxn];
int top,root;
/*debug部分
void travel(int r)
{
if(r)
{
travel(ch[r][0]);
printf("node: %2d l: %2d r: %2d pre: %2d val: %2d siz: %2d add: %2d sum: %2d\n",r,ch[r][0],ch[r][1],pre[r],val[r],siz[r],add[r],sum[r]);
travel(ch[r][1]);
}
}
void debug()
{
printf("root= %d\n",root);
travel(root);
}
*/
///newnode部分主要功能是为每个节点分配一个编号和初始化该节点信息,注意这里的引用
void newnode(int &x,int p,int v)
{
x=++top;
ch[x][0]=ch[x][1]=0;
pre[x]=p;
val[x]=v;
add[x]=0;
sum[x]=v;
siz[x]=1;
}
///和线段树一样的操作
void pushup(int x)
{
siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;
sum[x]=sum[ch[x][0]]+sum[ch[x][1]]+val[x];
}
void pushdown(int x)
{
if(add[x])
{
add[ch[x][0]]+=add[x];
add[ch[x][1]]+=add[x];
val[ch[x][0]]+=add[x];
val[ch[x][1]]+=add[x];
sum[ch[x][0]]+=(long long)siz[ch[x][0]]*add[x];
sum[ch[x][1]]+=(long long)siz[ch[x][1]]*add[x];
add[x]=0;
}
}
///由数列的中间开始建树
void build(int &x,int l,int r,int p)
{
int mid=(l+r)>>1;
newnode(x,p,tmp[mid]);
if(l<mid) build(ch[x][0],l,mid-1,x);
if(r>mid) build(ch[x][1],mid+1,r,x);
pushup(x);
}
///初始化终端节点,申请两个虚拟节点,建树
void init(int n)
{
for(int i=0; i<n; i++) scanf("%d",&tmp[i]);
root=top=0;
siz[0]=ch[0][0]=ch[0][1]=add[0]=sum[0]=pre[0]=0;
newnode(root,0,-1);
newnode(ch[root][1],root,-1);
build(keytree,0,n-1,ch[root][1]);
pushup(ch[root][1]);
pushup(root);
}
///旋转操作,kind代表旋转方式
void Rotate(int x,int kind)
{
int y=pre[x];
pushdown(y);
pushdown(x);
ch[y][!kind]=ch[x][kind];
pre[ch[x][kind]]=y;
if(pre[y]) ch[pre[y]][ch[pre[y]][1]==y]=x;
pre[x]=pre[y];
ch[x][kind]=y;
pre[y]=x;
pushup(y);
}
///将r节点旋转到goal下面,自底向上的旋转
void splay(int r,int goal)
{
pushdown(r);
while(pre[r]!=goal)
{
if(pre[pre[r]]==goal)
Rotate(r,ch[pre[r]][0]==r);
else
{
int y=pre[r];
int kind=ch[pre[y]][0]==y;
if(ch[y][kind]==r) ///之字形
{
Rotate(r,!kind);
Rotate(r,kind);
}
else///一字型
{
Rotate(y,kind);
Rotate(r,kind);
}
}
}
pushup(r);
if(goal==0) root=r;
}
///根据siz的特征找到第k号节点
int get_kth(int r,int k)
{
pushdown(r);
int t=siz[ch[r][0]]+1;///注意这里的+1
if(t==k) return r;
if(k<t) get_kth(ch[r][0],k);
else get_kth(ch[r][1],k-t);
}
///由于多了两个节点,所以每次将l旋转到0下面,r+2旋转到root下面,
///这样才能准确的确定keytree就是要找的区间,结合图形和get_kth想
long long query(int l,int r)
{
splay(get_kth(root,l),0);
splay(get_kth(root,r+2),root);
return sum[keytree];
}
void update(int l,int r,int d)
{
splay(get_kth(root,l),0);
splay(get_kth(root,r+2),root);
add[keytree]+=d;
val[keytree]+=d;
sum[keytree]+=(long long)siz[keytree]*d;
pushup(ch[root][1]);
pushup(root);
}
int main()
{
int n,q;
while(scanf("%d%d",&n,&q)!=EOF)
{
init(n);
char str[10];
while(q--)
{
// debug();
int a,b,c;
scanf("%s",str);
if(str[0]=='Q')
{
scanf("%d%d",&a,&b);
long long ans=query(a,b);
printf("%I64d\n",ans);
}
else
{
scanf("%d%d%d",&a,&b,&c);
update(a,b,c);
}
}
}
}