poj 1390 Blocks（记忆化搜索/动态规划）

程序设计实习递归练习 poj 1390 Blocks（记忆化搜索/动态规划）
总时间限制: 5000ms 内存限制: 65536kB

描述
Some of you may have played a game called ‘Blocks’. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a ‘box segment’. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

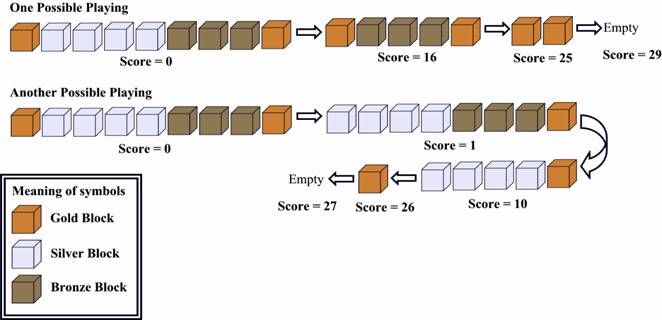
Now let’s look at the picture below:

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

输入
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

输出
For each test case, print the case number and the highest possible score.

样例输入
2
9
1 2 2 2 2 3 3 3 1
1
1

样例输出
Case 1: 29
Case 2: 1

来源
Liu Rujia@POJ

本题先朴素地想一想，可以转化为一个求解区间[l,r]上分数最大值的问题，又由于重复的子问题很多，所以可以考虑用记忆化搜索实现，应用动态规划思想。

首先得一个想法是既然求解[l,r]上分数最大值问题，那么不如列出一个函数f(l,r)来搜索，但是很快发现，同样是f(l,r)，与它右边的同色块颜色有关，所以一个维度似乎是不够的。接下来我曾经使用过一下一个方法垂死挣扎企图用两个维度解决问题，但是还是失败了，因为右边状态始终是一个独立的。

后来参考了别人的题解和教学ppt上，终于思考出了正确的算法，就是引入一个额外维度来确定右边状态。除了这个大方向意外，还有一些细节要考虑：
1.一开始应该预处理令相邻同色块合并成一个大块，用num[i],c[i]，记录大块中色块数目与颜色，用于减少搜索过程中对相邻同色块的搜索。
2.初始化时候为了减少时间开销可以考虑用memset(a,0,sizeof(a))，注意不要用错memset，不然不如不用，尤其注意第二个参数为按字节设置，第三个参数为总共需要初始化的字节数。

考虑函数f(l,r,len)，表示与r位同色的右边还有len个情况下[l,r]区间上的最大分数，那么容易知道，对于最右边无非两种策略，第一种是直接消去，第二种是和左边另一个同色块合并后再消去。那么容易写出dp状态转移方程式
f(l,r,len)=max{f(l,r-1,0)+(num[r]+len)*(num[r]+len),f(l,k,len+num[r])+f(k+1,r-1,0)(l<=k<=r-2 && c[k]==c[r])}
边界条件可以为l>r时返回0，也可以节省一次递归：l==r时f(l,r,len)=(num[r]+len)*(num[r]+len)

#define MAX_N 200

#include<stdio.h>
#include<memory.h>

int cases,n,m;
int color[MAX_N+1];
int num[MAX_N+1],c[MAX_N+1];
int max[MAX_N+1][MAX_N+1][MAX_N+1];

int f(int l,int r,int len)
{ 
    if (l==r)
        return max[l][r][len]=(num[r]+len)*(num[r]+len);
    if (max[l][r][len])
        return max[l][r][len];
    int temp=f(l,r-1,0)+(len+num[r])*(len+num[r]);
    for (int k=l;k<r;k++)
        if (c[k]==c[r]) 
            if (f(l,k,num[r]+len)+f(k+1,r-1,0)>temp)
                temp=f(l,k,num[r]+len)+f(k+1,r-1,0);
    return max[l][r][len]=temp;
}

int main()
{
    scanf("%d",&cases);
    color[0]=0;
    for (int loop=1;loop<=cases;loop++)
    {
        memset(max,0,sizeof(max));
        scanf("%d",&n);
        m=0;
        for (int i=1;i<=n;i++)
        {
            scanf("%d",&color[i]);
            if (color[i]==color[i-1])
                num[m]++;
            else
            {
                m++;
                c[m]=color[i];
                num[m]=1;
            }
        }
        printf("Case %d: %d\n",loop,f(1,m,0));
    }
    return 0;
}