字符串排列与八皇后问题

字符串排列问题

输入一个字符串，输出该字符串的所有排列。如输入abc，则输出abc,acb,bca,caab,cba.根据排列组合的知识，3个字符串的排列有3!=6个。

先考虑字符没有重复的情况：

可以将字符分成两个部分，第一部分为第一个字符，第二部分为后面的部分。

这样abc的排列情况可以这么分析：

a+bc;

b+ac;

c+ab;

即将第一个字符一次与后面的每一个字符交换，然后分别求剩余部分的排列。这种思想将原来为n的问题变成了n-1的问题。用递归实现：

下面是《剑指offer上的代码》：

/*输入一个字符串，打印改字符串中字符的所有排列，很多其他的问题
 * 可以转换成这个问题，如如何使正方体的对应面上数字的和相同，八皇后问题等
 */
void strPermutation(char * origin,char *pBegin);

void  strPermutation(char * origin){
	if(origin==NULL) return ;
	strPermutation(origin,origin);
}

//origin指向字符串起始的指针，pBegin指向每次需要修改的指针
void strPermutation(char * origin,char *pBegin)
{
	if(*pBegin=='\0')
	{
		std::cout<<origin<<std::endl;
	}else
	{
		for(char *pCh=pBegin;*pCh!='\0';pCh++)
		{
				char temp=*pCh;
				*pCh=*pBegin;
				*pBegin=temp;
				
				strPermutation(origin,pBegin+1);

				temp=*pCh;
				*pCh=*pBegin;
				*pBegin=temp;

		}
	}

}

int main()
{
	std::cout<<"字符串排列问题"<<std::endl;
	char  s[]="abc";
	strPermutation(s);
	return 0;
}

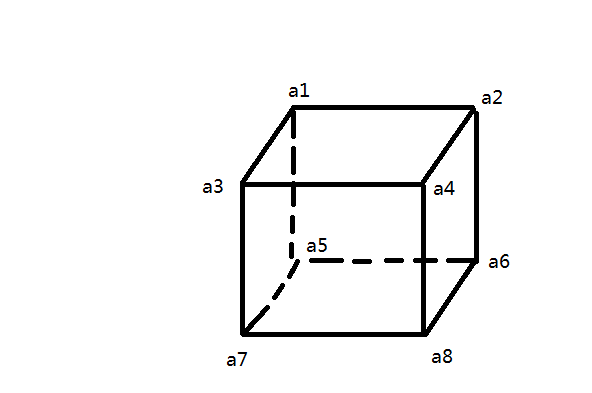
正方体上三组相对的面上的4个顶点的和相等和八皇后问题

解决了这个问题后很多其它的问题可以转化成这个问题，下面两个问题也是剑指offer上的题目：

输入一个含有8个数字的数组，判断有没有可能把这8个数字分别放到正方体的8个顶点上，使得正方体上三组相对的面上的4个顶点的和都相等。

这个问题实际上问的是是否存在a1-a8这样的一个组合，使得a1+a2+a3+a4==a5+a6+a7+a8,a1+a3+a5+a7==a2+a4+a6+8,a1+a2+a5+a6==a3+a4+a7+a8，这样和上面字符串的排列问题相比只有两点不同：

1.数据类型不同，字符串可以根据'\0'来判断字符串是否结束，对于数字构成的数组则需要一个表示数组长度的参数。

2.不是所有的排列都需要打印出来，只有符合上面条件的才需要打印出来。

同理，八皇后的问题和上面正方体的三组相对的面上顶点和相等这个问题基本上一致，只是判断条件不同。

八皇后问题如下：

在8*8的国际象棋盘上摆放8个皇后，使其不能互相攻击，即任意两个皇后不得处于同一行，同一列，或同意对角线上。那么符合条件的摆法有那些?

由于8个皇后不能出现在同一行，那么坑定是每一个皇后占据一行，那么可以定义一个数组ColumnIndex[8],数组中第i个数字表示位于第i行的皇后的列号，先把数组ColumnIndex用1-8的八个数字初始化，接下来对数组进行全排列。因为用不同的数字初始化数组，所以任意两个皇后肯定不在同一列，那么只需要判断任意两个皇后是否在同一个对角线上即可。及i-j==ColumnIndex[i]-ColumnIndex[j]或i-j==ColumnIndex[j]-ColumnIndex[i]是否成立即可。这就是八皇后问题的判断条件。

理解了区别之后代码就很容易了，改动也很小：其中judege是判断正方体三组对面的顶点和是否相等的函数，eightQueen是判断是否符合8皇后位置的函数，只需要在numPermutation中改变下判断条件，输出的就是符合条件的解。

#include "util.h"

void numPermutation(int *num,int *pBegin,int len);

//正方体中三组对象相等的判断函数
bool judge(int *num,int len);

//符合8皇后位置的组合
bool eightQueen(int *num,int len);

void numPermutation(int * num,int len)
{
	if(num==NULL) return ;
	numPermutation(num,num,len);
}
void numPermutation(int *num,int *pBegin,int len)
{
	if((pBegin-num)==len)
	{
		if(judge(num,len))
		{
			//打印数组的内容
			printArrayT(num,len);
		}
				
	}
	else
	{
		for(int* i=pBegin;i<pBegin+len-(pBegin-num);i++)
		{
			int tmp=*pBegin;
			*pBegin=*i;
			*i=tmp;

			numPermutation(num,pBegin+1,len);
			
			tmp=*i;
			*i=*pBegin;
			*pBegin=tmp;

		}

	}

}

bool judge(int *num,int len)
{
	if(num==NULL||len!=8) return false;
	if((num[0]+num[1]+num[2]+num[3])==(num[4]+num[5]+num[6]+num[7])&&
					(num[0]+num[2]+num[4]+num[6])==(num[1]+num[3]+num[5]+num[7])&&
					(num[0]+num[1]+num[4]+num[5])==(num[2]+num[3]+num[6]+num[7]))
			return true;
	return false;
}

bool eightQueen(int *num,int len)
{
	if(num==NULL||len!=8) return false;
		for(int i=0;i<len;i++)
		{
			for(int j=0;j<len;j++)
			{
				if(i!=j)
				{
					if((i-j)==(num[i]-num[j])||(i-j)==(num[j]-num[i]))
							return false;
				}
			}
		}
		return true;
}
int main()
{
	int arr[]={1,2,3,4,5,6,7,8};
	numPermutation(arr,sizeof(arr)/sizeof(arr[0]));
	return 0;
}

//打印数组
template<class T>
void printArrayT(T * t,int len){
	for(int i=0;i<len;i++)
			std::cout<<t[i]<<" ";
	std::cout<<std::endl;
}

消除重复字符

上面都是讨论的字符串中没有重复字符的情况，如果字符串中有重复字符，还是借助于上面的思想，应该是在某些情况下不进行递归查询了

以字符abbc举例：

首先将字符分割成两个部分，第一个字符和剩下的字符，然后将第一个字符依次与后面的字符互换

a+bbc

b+abc

b+bac

c+bba

上面4种替换方案中第2种和第3中会出现重复，第2中方方案中abc和第三种方案中bac的排列是相同的（这就是上面没有重复的字符的全排列问题，共有3!=6种排列方案），那么可以将第3种方案舍弃掉，换成一般的术语就是如果存在与被替换的字符相同的字符，那么不需要对这个字符进行替换并求解全排列。图示如下图：

代码如下：

#include  <iostream>
#include <stdlib.h>
#include <stdio.h>


/*输入一个字符串，打印改字符串中字符的所有排列，很多其他的问题
 * 可以转换成这个问题，如如何使正方体的对应面上数字的和相同，八皇后问题等
 */


//判断是否交换的函数
bool is_swap(char * begin,char *end);

//交换两个指针指向的变量的函数
void swap(char * p1,char *p2);

//字符串排列函数
void strPermutation(char * origin,char *pBegin);

void  strPermutation(char * origin){
	if(origin==NULL) return ;
	strPermutation(origin,origin);
}

//origin指向字符串起始的指针，pBegin指向每次需要修改的指针
void strPermutation(char * origin,char *pBegin)
{
	if(*pBegin=='\0')
	{
		std::cout<<origin<<std::endl;
	}else
	{
		//pBegin指向的是字符串中元素只有一个的部分,pCh指向的是字符串中的剩余部分
		for(char *pCh=pBegin;*pCh!='\0';pCh++)
		{
				if(is_swap(pBegin,pCh))	
				{
					swap(pBegin,pCh);//交换pBegin和pCh

					strPermutation(origin,pBegin+1);

					swap(pBegin,pCh);//交换pBegin和pCh
				}
		}
	}

}

//判断是否交换，如果[begin,end)区间内存在与end指针指向相同的值，返回false表示不需要交换
bool is_swap(char * begin,char * end)
{
	bool flag=true;
	for(char *p=begin;p<end;p++)
	{
		if(*p==*end) flag=false;
	}
	return flag;
}

//交换两个指针指向的值
void swap(char * p1,char *p2){
	char tmp=*p1;
	*p1=*p2;
	*p2=tmp;
}
int main()
{
	std::cout<<"消除重复字符串排列问题"<<std::endl;
	char  s[]="abbc";
	strPermutation(s);
	return 0;
}

abbc所有组合的个数用数学公式计算为A44/A22=12，输出结果也是有12组无重复的排列。