实现二叉搜索树--查找、插入、删除
- 每个节点都有一个作为搜索依据的关键码(key),所有节点的关键码互不相同。
- 左子树上所有节点的关键码(key)都小于根节点的关键码(key)。
- 右子树上所有节点的关键码(key)都大于根节点的关键码(key)。
- 左右子树都是二叉搜索树。
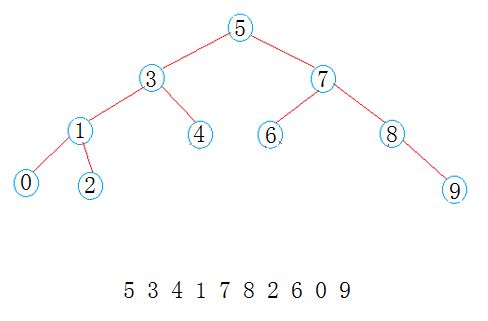
下图就是一棵二叉搜索树
二叉搜索树有查找,插入,删除等操作,每个操作可以通过递归或非递归实现。
插入:
1、若搜索树为空则new一个节点作为根节点;
2、若要插入的节点等于根节点,返回false;
3、若要插入的节点大于根节点,递归右子树插入节点,反之递归左子树插入节点。
查找:
1、若搜索树为空则返回空;
2、若要查找的节点等于根节点,返回根节点;
3、若要查找的节点大于根节点,递归查找右子树,反之递归查找左子树。
删除:
1、若搜索树为空则返回false;
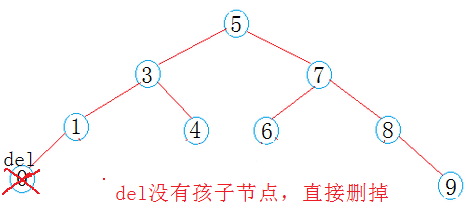
2、若待删除的节点没有左右孩子,直接删除该节点;
3、若待删除的节点只有一个孩子:
(1)若del 的左孩子为空,
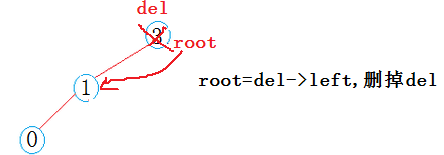
a: 若del==root,让root=del->right,然后删掉del;
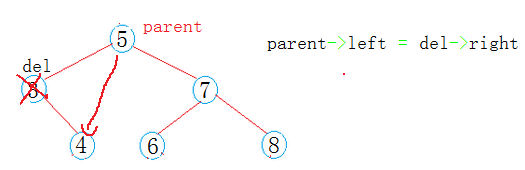
b: 若del是parent的左孩子(del == parent->left),让parent的左孩子指向del的右孩子(parent->left = del->right;);
c: 若del是parent的右孩子(del ==parent->right),让parent的右孩子指向del的右孩子(parent->right = del->right;);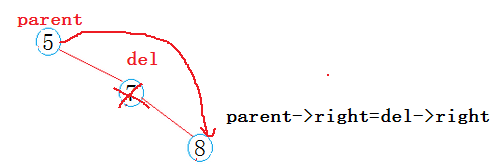
(2)若del 的右孩子为空,
a: 若del==root,让root=del->left,然后删掉del;
b: 若del是parent的左孩子(del == parent->left),让parent的左孩子指向del的左孩子( parent->_left = del->_left);
c: 若del是parent的右孩子(del == parent->right),让parent的右孩子指向del的左孩子(parent->right = del->left);
4、待删除节点有两个孩子:
第一步:先找到右子树的最左节点(保证了比del左子树所有节点都大,比del右子树其他节点都小);
第二步:交换最左节点和del的值(在第一步的基础上,交换后还是二叉搜索树);
第三步:删除最左节点(问题转化成了只有一个孩子的情况)
#pragma once
template<class K,class V>
struct BSTreeNode
{
K _key; //用于排序
V _val; //该节点包含的值
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
BSTreeNode(const K& key, const V& val)
: _key(key)
, _val(val)
, _left(NULL)
, _right(NULL)
{}
};
template<class K,class V>
class BSTree
{
public:
BSTree()
:_root(NULL)
{}
BSTreeNode<K, V>* Find_NR(const K& key) //非递归实现
{
while (_root)
{
//将key和根节点的key比较,如果大于,那么就在根节点的右边查找
if (key > _root->_key)
{
_root = _root->_right;
}
//将key和根节点的key比较,如果小于,那么就在根节点的左边查找
else if (key < _root->_key)
{
_root = _root->_left;
}
else
{
return _root;
}
}
return NULL;
}
BSTreeNode<K,V>* Find_R(const K& key) //递归
{
return _Find(_root, key);
}
bool Insert_NR(const K& key, const V& val)
{
if (_root == NULL)
{
_root = new BSTreeNode<K, V>(key,val);
}
else
{
BSTreeNode<K, V>* cur = _root;
BSTreeNode<K, V>* parent = NULL;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key<cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
if (key>parent->_key)
{
parent->_right = new BSTreeNode<K, V>(key, val);
}
else
{
parent->_left = new BSTreeNode<K, V>(key,val);
}
}
return true;
}
bool Insert_R(const K& key, const V& val)
{
if (_root == NULL)
{
_root =new BSTreeNode<K, V>(key,val);
return true;
}
return _Insert(_root,key,val);
}
bool Delete_NR(const K& key)
{
if (_root == NULL)
{
return false;
}
BSTreeNode<K, V>* del = _root;
BSTreeNode<K, V>* parent = NULL;
while (del)
{
if (del->_key > key)
{
parent = del;
del = del->_left;
}
else if (del->_key < key)
{
parent = del;
del = del->_right;
}
else
{
break;
}
}
if (del)
{
//最多一个孩子
if (del->_left == NULL) //左孩子为空
{
if (del == _root)
{
_root = del->_right;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_right;
}
else
{
parent->_right = del->_right;
}
}
delete del;
del = NULL;
return true;
}
else if (del->_right == NULL) //右孩子为空
{
if (del == _root)
{
_root = del->_left;
}
else
{
if (del == parent->_left)
{
parent->_left = del->_left;
}
else
{
parent->_right = del->_left;
}
}
delete del;
del = NULL;
return true;
}
else //两个孩子
{
parent = del;
BSTreeNode<K, V>* firstLeft = del->_right;
//找右子树的最左节点
while (firstLeft->_left)
{
parent = firstLeft;
firstLeft = firstLeft->_left;
}
swap(firstLeft->_key, del->_key);
swap(firstLeft->_val, del->_val);
if (firstLeft == parent->_left)
{
parent->_left = firstLeft->_right;
}
else
{
parent->_right = firstLeft->_right;
}
delete firstLeft;
firstLeft = NULL;
return true;
}
}
return false;
}
bool Delete_R(const K& key)
{
return _Delete(_root, key);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
protected:
BSTreeNode<K, V>* _Find(BSTreeNode<K, V>*& root, const K& key)
{
if (NULL == root)
{
return false;
}
if (key > root->_key)
{
_Find(root->_right, key);
}
else if (key < root->_key)
{
_Find(root->_left, key);
}
else
{
return root;
}
}
bool _Insert(BSTreeNode<K, V>*& root, const K& key, const V& val)
{
if (root == NULL)
{
root = new BSTreeNode<K, V>(key, val);
return true;
}
if (root->_key > key)
{
return _Insert(root->_left,key,val);
}
else if (root->_key < key)
{
return _Insert(root->_right, key, val);
}
else
{
return false;
}
return true;
}
bool _Delete(BSTreeNode<K, V>*& root, const K& key)
{
if (NULL == root)
{
return false;
}
if (key > root->_key)
{
return _Delete(root->_right, key);
}
else if (key < root->_key)
{
return _Delete(root->_left, key);
}
else
{
BSTreeNode<K, V>* del = root;
if (root->_left == NULL)
{
root = root->_right;
}
else if (root->_right == NULL)
{
root = root->_left;
}
else
{
BSTreeNode<K, V>* firstLeft = root->_right;
while (firstLeft->_left)
{
firstLeft = firstLeft->_left;
}
swap(del->_key, firstLeft->_key);
swap(del->_val, firstLeft->_val);
return _Delete(root->_right, key);
}
}
}
void _InOrder(BSTreeNode<K, V>* root)
{
if (NULL == root)
{
return;
}
_InOrder(root->_left);
cout << root->_val << " ";
_InOrder(root->_right);
}
private:
BSTreeNode<K, V>* _root;
};
#include<iostream>
using namespace std;
#include"BinarySearchTree.hpp"
int main()
{
BSTree<int,int> bst;
bst.Insert_NR(1, 1);
bst.Insert_NR(2, 2);
bst.Insert_NR(3, 3);
bst.Insert_NR(4, 4);
bst.Insert_NR(6, 6);
bst.InOrder();
bst.Delete_NR(6);
bst.Delete_NR(2);
bst.Delete_NR(3);
bst.Delete_NR(4);
bst.InOrder();
bst.Insert_R(1, 1);
bst.Insert_R(2, 2);
bst.Insert_R(3, 3);
bst.Insert_R(4, 4);
bst.Insert_R(6, 6);
bst.InOrder();
bst.Delete_R(6);
bst.Delete_R(2);
bst.Delete_R(3);
bst.Delete_R(4);
bst.InOrder();
return 0;
}