树和二叉树的基本运算实现-哈夫曼树/哈夫曼编码

问题及代码：

设计一个程序exp7-6.cpp，构造一棵哈夫曼树，输出对应的哈夫曼编码和平均查找长度。并用表7.8所示的数据进行验证。

表7.8 单词及出现的频度

单词	The	of	a	to	and	in	that	he	is	at	on	for	His	are	be
出现频度	1192	677	541	518	462	450	242	195	190	181	174	157	138	124	123

/*
* Copyright (c) 2016, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称：Huffman.cpp
* 作    者：单昕昕
* 完成日期：2016年6月13日
* 版 本 号：v1.0
*/
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define inf 999999
#define MAXN 100

typedef struct//树中每个节点的类型
{
    string data;//节点值
    double weight;//权重
    int parent,lchild,rchild;//双亲和左右孩子节点
} HTNode;
HTNode ht[MAXN];

typedef struct//存放每个节点哈夫曼编码的结构
{
    char cd[MAXN];//存放当前节点的哈夫曼编码
    int start;//存放该节点哈夫曼编码的起始位置，编码为cd[start]~cd[n]
} HCode;
HCode hcd[MAXN];

void CreateHT(HTNode ht[],int n)//构造哈夫曼树
{
    int i,k,lnode,rnode;
    double min1,min2;
    for(i=0; i<2*n-1; ++i)
        ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
    for(i=n; i<2*n-1; ++i)
    {
        min1=min2=inf;
        lnode=rnode=-1;
        for(k=0; k<=i-1; ++k)
            if(ht[k].parent==-1)
            {
                if(ht[k].weight<min1)
                {
                    min2=min1;
                    rnode=lnode;
                    min1=ht[k].weight;
                    lnode=k;
                }
                else if(ht[k].weight<min2)
                {
                    min2=ht[k].weight;
                    rnode=k;
                }
            }
        ht[i].weight=ht[lnode].weight+ht[rnode].weight;
        ht[i].lchild=lnode;
        ht[i].rchild=rnode;
        ht[lnode].parent=i;
        ht[rnode].parent=i;
    }
}

void CreateHCode(HTNode ht[],HCode hcd[],int n)//根据哈夫曼树求哈夫曼编码
{
    int i,f,c;
    HCode hc;
    for(i=0; i<n; ++i)
    {
        hc.start=n;
        c=i;
        f=ht[i].parent;
        while(f!=-1)
        {
            if(ht[f].lchild==c)
                hc.cd[hc.start--]='0';
            else
                hc.cd[hc.start--]='1';
            c=f;
            f=ht[f].parent;
        }
        hc.start++;
        hcd[i]=hc;
    }
}

void Display(HTNode ht[],HCode hcd[],int n)
{
    int i,k;
    int sum=0,m=0,cnt;
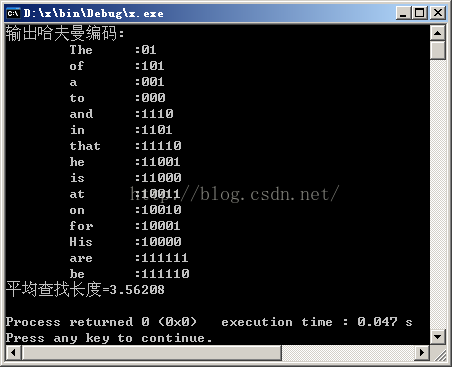
    cout<<"输出哈夫曼编码:"<<endl;
    for (i=0; i<n; i++)
    {
        cnt=0;
        cout<<"\t"<<ht[i].data<<"\t"<<":";
        for (k=hcd[i].start; k<=n; k++)
        {
            cout<<hcd[i].cd[k];
            cnt++;
        }
        m+=ht[i].weight;
        sum+=(ht[i].weight*cnt);
        cout<<endl;
    }
    cout<<"平均长度="<<1.0*sum/m<<endl;
}

int main()
{
    int n=15;
    string str[n]= {"The","of","a","to","and","in","that","he","is","at","on","for","His","are","be"};
    int frq[n]= {1192,677,541,518,462,450,242,195,190,181,174,157,138,124,123};
    for (int i=0; i<n; i++)
    {
        ht[i].data=str[i];
        ht[i].weight=frq[i];
    }
    CreateHT(ht,n);
    CreateHCode(ht,hcd,n);
    Display(ht,hcd,n);
    return 0;
}

运行结果：