图基本算法 图搜索基于邻接表的（广度优先、深度优先）

BFS   

注：以下代码均为部分，关于图的表示方法参看我的博客—图的存储：

 

一、广度优先搜索

　　广度优先搜索（BFS）是最简单的图搜索算法之一，也是很多重要的图算法的原型。在Prim最小生成树算法和Dijkstra单源最短路径算法中，都采用了与广度优先搜索类似的思想。

　　在给定图G=(V,E)和一个特定的源顶点s的情况下，广度优先搜索系统地探索G中的边，以期发现可以从s到达的所有顶点，并计算s到所有这些可达顶点之间的距离（即最少的边数）。该搜索算法同时还能生成一棵根为s、且包括所有s的可达顶点的广度优先树。对从s可达的任意顶点v，广度优先树中从s到v的路径对应于图G中从s到v的一条最短路径，即包含最少边数的路径。该算法对有向图和无向图同样适用。之所以称为广度优先搜索，是因为它始终是将已发现和未发现顶点之间的边界，沿其广度方向向外扩展。亦即，算法首先发现和s距离为k的所有顶点，然后才会发现和s距离为k+1的其他顶点。

　　在广度优先搜索中，我们首先要注意一个顶点的3种状态：

　　已到达（已访问）但还未考察：表示当前搜索到的这个顶点，接下来要对这个顶点进行分析。

　　正在考察：已经到达了这个顶点，但是它的相邻顶点还没有完全被访问到，称为未考察完成。采用队列存储未被考察的顶点。

　　已考察：已经到达了这个顶点，且它的所有相邻顶点都已经被访问完成，则称该顶点已考察。

　　具体步骤如下:

　　（1）从顶点s开始，标记它为已访问，将其压入队列中；

　　（2）这时，顶点s的的相邻顶点还未被访问，所以s暂时还为未考察状态；

　　（3）访问它的所有相邻顶点，并将它们压入队列，之后s的状态变为已考察，将其从队列中删除；这些入队的顶点的父亲顶点即为s

　　（4）取队头顶点，以其为起点重复进行以上操作。当所有的顶点都被考察完毕，即队列为空时，考察停止。

　　由分析可知，广度优先搜索的总运行时间为O(V+E)，为一个线性时间。

 　　

      最短路径：源顶点为s，d[v]中保存从s到v的最短路径长度

      广度优先树：过程BFS在搜索图的同时，也建立了一棵广度优先树，这棵树是用parent[]表示的，parent[v]表示的是顶点v的父亲结点。

广度优先搜索C++（邻接表）实现：

#define INF 9999
bool visited[maxn];         //标记顶点是否被考察，初始置为false
int d[maxn], parent[maxn];  //d[]记录最短路径长度，parent[]记录某结点的父亲结点，生成树
void bfs(int s)             //广度优先搜索，邻接表输入（详见“一、图的表示”）
{
    for(int i = 1; i <= n; i++) //初始化
    {
        d[i] = INF;
        parent[i] = -1;
        visited[i] = false;
    }
    visited[s] = true;
    d[s] = 0;
    queue<int> q;        //用STL队列实现 ，#include <queue>
    q.push(s);           //压入队列
    while(!q.empty())
    {
        int u = q.front();          //取队头元素
        arcnode * p = Ver[u].firarc;
        while(p != NULL)        //遍历相邻顶点
        {
            if(!visited[p->vertex])
            {
                q.push(p->vertex);  //压入队列
                parent[p->vertex] = u;  //指向父亲
                d[p->vertex] = d[u]+1;  //路径长+1
                visited[p->vertex] = true;   //置为已被考察
            }
            p = p->next;
        }
        q.pop();        //出队列
    }
}
void PrintPath(int s, int v)    //打印从s到v的最短路径，需先调用bfs(s)
{
    if(v == s)
        cout << s << endl;
    else if(parent[v] == -1)
        return;
    else
    {
        PrintPath(s,parent[v]);
        cout << v << endl;
    }
}

DFS

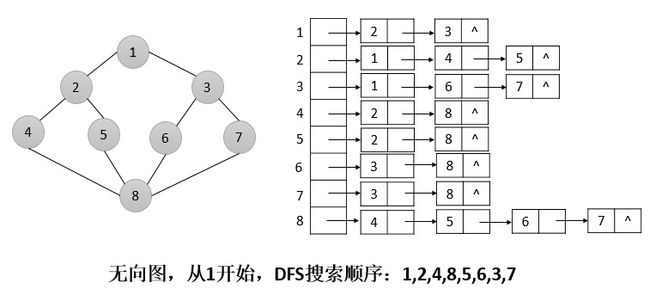
二、深度优先搜索

　　深度优先搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。在深度优先搜索中，对于最新发现的顶点，如果它还有以此为起点而未探测到的边，就沿此边继续探测下去。当顶点v的所有边都已被探寻过后，搜索将回溯到发现顶点v有起始点的那些边。这一过程一直进行到已发现从源顶点可达的所有顶点时为止。如果还存在未被发现的顶点，则选择其中一个作为源顶点，并重复以上过程。整个过程反复进行，直到所有的顶点都已被发现为止。

　　与广度优先搜索类似，在深度优先搜索中，每当扫描已发现顶点u的邻接表，从而发现新顶点v时，就将置v的父域parent[v]为u。与广度优先搜索不同的是，其先辈子图形成一棵树，深度优先搜索产生的先辈子图可以由几棵树所组成，因为搜索可能由多个源顶点开始重复进行。深度优先搜索的先辈子图形成了一个由数棵深度优先树所组成的深度优先森林。

　　除了创建一个深度优先森林外，深度优先搜索同时为每个顶点加盖时间戳。每个顶点v有两个时间戳：当顶点v第一次被发现时，记录下第一个时间戳d[v]，当结束检查v的邻接表时，记录下第二个时间戳f[v]。许多图的算法都用到了时间戳，它们对推算深度优先搜索的进行情况有很大帮助。

　　具体步骤如下：
　　　　（1）初始化：将所有顶点置为未访问，其父亲结点均为-1

　　　　（2）遍历每一个顶点u，如果它未访问，则对该顶点进行（3）操作

　　　　（3）置该顶点u为正在访问。对于u的每一个相邻顶点v，如果v未被访问，对v重复（3）操作，直至找到所有相邻顶点为止。置顶点u为已访问。

　　　　（4）若所有的顶点都被考察，则搜索停止。

深度优先搜索C++（邻接表）实现：

#define INF 9999
bool visited[maxn];         //标记顶点是否被考察，初始值为false
int parent[maxn];           //parent[]记录某结点的父亲结点，生成树，初始化为-1
int d[maxn], time, f[maxn]; //时间time初始化为0，d[]记录第一次被发现时，f[]记录结束检查时
void dfs(int s)             //深度优先搜索（邻接表实现），记录时间戳，寻找最短路径
{
    cout << s << " ";
    visited[s] = true;
    time++;
    d[s] = time;
    arcnode * p = Ver[s].firarc;
    while(p != NULL)
    {
        if(!visited[p->vertex])
        {
            parent[p->vertex] = s;
            dfs(p->vertex);
        }
        p = p->next;
    }
    time++;
    f[s] = time;
}
void dfs_travel()       //遍历所有顶点，找出所有深度优先生成树，组成森林
{
    for(int i = 1; i <= n; i++)     //初始化
    {
        parent[i] = -1;
        visited[i] = false;
    }
    time = 0;
    for(int i = 1; i <= n; i++)     //遍历
        if(!visited[i])
            dfs(i);
    cout << endl;
}