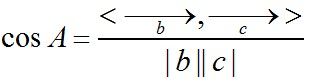词权重计算及应用
1 归一化
在讨论词权重和向量空间模型前需要先了解下归一化的概念。归一化(normailization)方法有两种形式。第一种形式是把数变为(0,1)之间的小数,方便计算。第二种是把有量纲(量纲是指单位)表达式变为无量纲表达式,这样归一化后统一了单位,方便比较,而且归一化后比较的数值才有意义。
2 词权重表示TF-IDF
词频-逆文档频率(term frequency-inverse document frequency,TF-IDF) 的概念被公认为信息检索中最重要的发明。在搜索、文献分类和其他相关领域有广泛的应用。
在计算机中光有词是不能计算的,需要把词转换为数字,这个数字能代表该词对文档中的重要程度,这个数字就是词的权重。权重的设定必须满足下面两个条件:
1)一个词预测主题能力越强,权重就越大,反之,权重就越小。我们在网页中看到“云计算”这个词,或多或少地能了解网页的主题。我们看到“应用”一次,对主题基本上还是一无所知。因此,“云计算“的权重就应该比”应用“大。
2) 应删除词(如的等停顿词)的权重应该是零。
2.1 词频
如果用词项t在文档d中出现的次数来表示词频,那么包含某些词多的文档应该比包含它们少的文档相关。当然,这个办法有一个明显的漏洞,就是长的文档比短的文档占便宜,因为长的文档总的来讲包含的关键词要多些。因此我们需要根据文档的长度,对关键词的次数进行归一化,也就是用关键词的次数除以文档的总字数。我们把这个商称为词的频率(term frequency,TF)。
2.2逆文档频率
如果一个关键词只在很少的文档中出现,我们通过它就容易锁定搜索目标,它的权重也就应该大。反之如果一个词在大量文档中出现,我们看到它仍然不很清楚要找什么内容,因此它应该小。概括地讲,假定一个关键词t在Dt个文档中出现过,那么Dt越大,t的权重越小,反之亦然。在信息检索中,使用最多的权重是逆文档频率(Inversedocument frequency 缩写为IDF),它的公式为
IDF=log(D/Dt)
其中D是全部文档数。比如,我们假定中文文档数是D=10亿,应删除词“的”在所有的文档中都出现,即 Dt=10亿,那么它的IDF=log(10亿/10亿)= log(1) = 0。假如专用词“云计算”在两百万个文档中出现,即Dw=200万,则它的权重IDF=log(500) =6.2。又假定通用词“应用”,出现在五亿个文档中,它的权重IDF= log(2)则只有 1。也就只说,在文档中找到一个“云计算”的比配相当于找到九个“应用”的匹配。
2.3 TF-IDF权重计算
对于每篇文档中的每个词(一般是指关键字及特征向量),可以将其TF和IDF组合在一起形成每个词最终的权重,计算公式如下
TF-IDF=TF*IDF
TF-IDF按照如下的方式对文档d中的词项t赋予权重:
(1)当t只在少数几篇文档中多次出现时,权重取值最大(此时能够对这些文档提供最强的区分能力);
(2)当t在一篇文档中出现次数很少,或者在很多文档中出现,权重取值次之(此时对最后的相关度计算作用不大);
(3)如果t在所有文档中都出现,那么权重取值最小。
3 向量空间模型
通过用TF-IDF表示词的权重,就可以把文档看成是一个向量(vector),其中的每个分量都对应词典中的一个词,分量值为词的权重值(可用TF-IDF计算,也有其他方法计算权重值)。当某词在文档中没有出现时,其对应的分量值为0。这种向量形式对于评分和排序十分重要。一系列文档在同一向量空间中的表示被称为向量空间模型(vector space model,简称VSM),它是信息检索领域一系列相关处理的基础,比如文档的评分、文档的分类及聚类。
用向量空间模型,一组文档的集合可以看成向量空间中的多个向量,每个词对应一个坐标轴,文档在每个坐标轴上的值是对应词的权重Weight。那么文档d对应的向量为
![]()
4 应用
4.1 文档相关性
(1)简单的文档相关性计算,可以用文档中的每个词的权重(TF-IDF)加权求和,即
TF1*IDF1 + TF2*IDF2 +... + TFN*IDFN。
(2)用余弦定理判断文档相似度
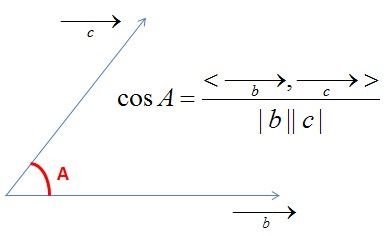
学过向量代数的人都知道,向量实际上是多维空间中有方向的线段。如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角了。可以用余弦定理判定文档的相似度。
余弦定理对我们每个人都不陌生,它描述了三角形中任何一个夹角和三个边的关系,换句话说,给定三角形的三条边,我们可以用余弦定理求出三角形各个角的角度。假定三角形的三条边为 a, b 和 c,对应的三个角为 A, B 和 C,那么角 A 的余弦为
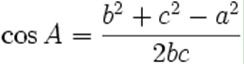
如果我们将三角形的两边 b 和 c 看成是两个向量,那么上述公式等价于
其中分母表示两个向量 b 和 c 的长度,分子表示两个向量的内积。
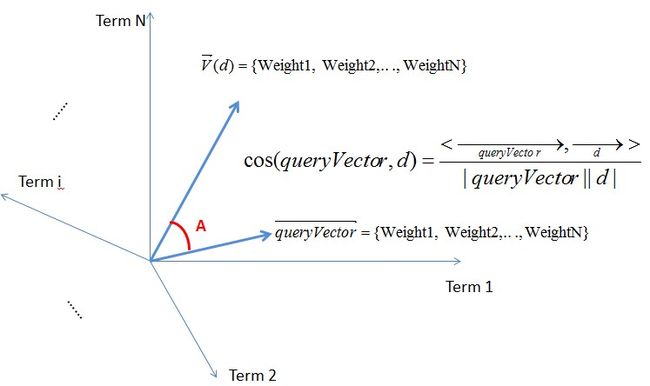
同样在向量空间下,可以用余弦定理对两篇文档的相似度进行计算,如下图
举一个具体的例子(这个例子来自《数学之美》),假如文章 X 和文章 Y 对应向量分别是x1,x2,...,x64000 和y1,y2,...,y64000,那么它们夹角的余弦等于,
余弦定理应用
1)分类
如果两篇文档的特征向量相近,则对应的文档内容相似,它们应当归在一类,反之亦然。由于向量中的每一个变量都是正数,因此余弦的取值在0和1之间。当两条文章向量夹角的余弦等于1时,这两条文章完全重复(用这个办法可以删除重复的文档);当夹角的余弦接近于1时,两条文章相似,从而可以归成一类;夹角的余弦越小,两条文章越不相关。
2)推荐搜索
如果在某个系统中,用户确定一篇文档然后查找与之相似的我的那个,那么上面的文档相似度计算就非常有用。在一些搜索引擎的返回结果当中有时就看到这种搜索方式,比如一些搜索引擎的more like this(类似网页)按钮,这些现象在我们现实生活中非常常见,如网上购物,搜索引擎会自动向用户推荐商品,即所谓的推荐搜索。下图是亚马逊根据用户浏览记录推荐的书
当然,工程实现上还会用到很多处理算法,但是基本思想是用余弦定理评定相关性。
3)查询结果排名
将文档表示成向量的一个令人信服的理由是可以将查询表示成向量。可以将查询看成一篇极端的文档来处理,因此,可以哦通过计算给定的查询向量和每个文档向量的相似度来对符合查询结果的文档进行排名,最终的结果可以选择排名靠前的一些文档。下图queryVector为查询向量。
搜索引擎常用的文档排名算法有Google的PageRank。PageRank的核心思想:在互联网上,如果一个文档被很多其他文档所链接,说明它受到普遍的承认和信赖,那么它的排名就高。一个文档的排名是来自于所有指向这个文档的其他文档的权重(这些文档的本身排名)之和。如果结合文档排名算法,那么给定一个查询,有关文档的综合排序大致由相关性和文档排名的乘积决定。
开源全文检索库Lucene的排名和打分算法可见 Lucene打分公式的数学推导
参考文献
Introduction to Information Retrieval,信息检索导论,Christopher D.Manning / Hinrich Schütze/ Prabhakar Raghavan
数学之美,吴军