哈弗曼树与哈弗曼树编码
在哈夫曼树的定义中,涉及到了路径、路径长度、权等概念,下面先给出概念的定义。
一、概念与定义
路径:从树的一个结点到另一个结点的分支构成这两个结点之间的路径,对于哈夫曼树特指从根节点到某节点的路径。
路径长度:路径上的分支数目叫做路径长度。树的路径长度:从树根到每一结点的路径长度之和。
权:赋予某一个事物的一个量,是对事物的某个或某些属性数值化描述。在数据结构中,包括结点和边两大类,所以对应有结点权和边权。其具体代表的意义有具体情况而定。
结点的带权路径长度:从树根到结点之间的路径长度与结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和(WPL--weighted path length)。它的权值分别为![]() ,从根到各叶子结点的路径长度分别为
,从根到各叶子结点的路径长度分别为![]() 。则其带权路径长度WPL通常记作:
。则其带权路径长度WPL通常记作:
WPL的计算如下所示:
对于图a:WPL=2*(9+8+1+6)=48;
对于图b:WPL=8*1+9*2+(1+6)*3=47;
对于图c:WPL=9*1+8*2+(1+6)*3=46;
由图可以看出,权值越大的结点离根节点越近。
二、哈夫曼树构造算法
哈弗曼树的构造步骤:
1、根据给定的n个权值(w1,w2,w3,....wn),构造n棵只有根结点的二叉树,令起权值为wj;
2、在森林中选取两棵根结点权值最小的树作为左右子树,构造一棵新的二叉树,置新二叉树根结点权值为其左右子树根结点权值之和
3、在森林中删除这两棵树,同时将新得到的二叉树加入森林中;
4、重复上述两个步骤,最后构成的树即为哈弗曼树。
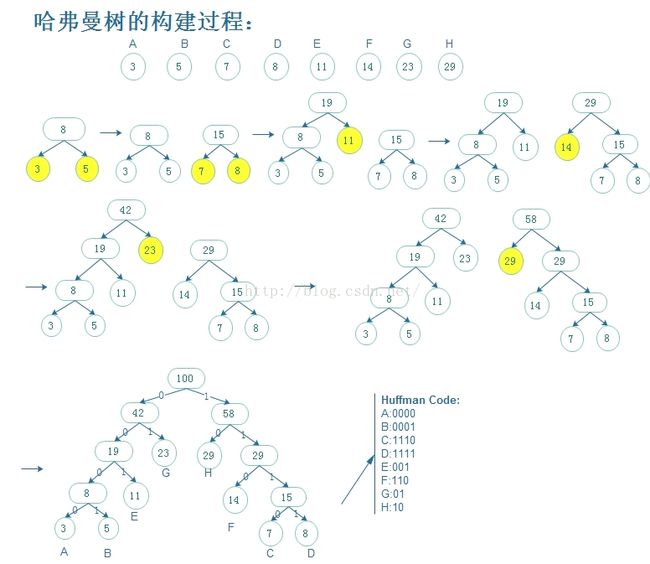
下图显示了构造一棵哈弗曼树的两种方法:
常见的构造比较简单,这里我选择了两种比较特殊的数据进行了构造:
哈弗曼树并行生长的原则:如果新形成的二叉树的根节点的值大于或等于森林中的另外两个只有根结点树的值,那么接下来的两棵树将并行生长。并不是线性的直接向上生长。
构造方法一:
构造方法二:
最后显示了哈夫曼树的编码,编码的原则左小右大。
三、哈夫曼树在编码中的应用
哈夫曼树最常应用的地方就是对报文进行编码传输通信。在数据的交流中,我们对数据是有要求的:
(1)解码结果与发送方发送的电文完全一样。也就是说发送方传输的二进制编码,到接收方解码后必须具有唯一性;
(2)为了传输的效率和网络的通信及时占用资源少,发送的二进制编码尽可能地短。
下面介绍两种编码方式:
1. 等长编码
这种编码方式的特点是每个字符的编码长度相同,编码长度就是每个编码被翻译的二进制位数。假设字符集只含有4个字符A,B,C,D,用二进制两位表示的编码分别为00,01,10,11。 若现在有一段电文为:ABACCDA,则应发送二进制序列:000100101011000111,总长度为16位。当接收方接收到这段电文后,将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性,但是存在的问题是编码长度并不是最短的,不满足上面的(2)的要求,因为在大数据量的情况下,我们必须的考虑效率问题,那么如何得到最短的编码呢?使用哈夫曼树就可以解决这个问题。这里先介绍一个前缀吗的概念。
前缀码:如果在一个系统中,任意一个编码都不是其他任何编码的前缀(最左子串),则称此编码系统中的编码是前缀码。
例如:(A:110、B:111、C:10、D:0)就是前缀码。但是(A:110、B:11、C:00、D:0)就不是前缀码。0是00的前缀,11是110的前缀。如果不定长的编码不是前缀码,则在译码时会产生二义性。例如110是A呢?还是BD呢?所以对于不定长编码一定要是前缀码。
2. 不等长编码
不等长编码可以叫最优的前缀码。在传送报文时,为了使其二进制位数尽可能地少,可以将每个字符的编码设计为不等长的, 使用频度较高的字符分配一个相对比较短的编码,使用频度较低的字符分配一个比较长的编码。如何得到最优的前缀编码呢?我们就可以利用上述的哈夫曼树来设计,同常成这种编码为哈夫曼编码,它不仅减少电文的总长,还必须考虑编码的唯一性。
四、哈夫曼树中的唯一和不唯一
唯一:哈夫曼树的WPL一定是最小的,唯一,最优是不变的。
不唯一:编码不唯一(表现出来就是形态不唯一)。比如说左小右大,或者是左大右小,树枝左右顺序是可以交换的,也就是说所得的哈夫曼编码则可能不同。