stirling 数
组合数学中的stirling数有两类,第一类,数字有正负,绝对值是包含n个元素的集合分作k个环排列的方法个数;第二类是把包含n个元素的集合划分成k个非空子集的方法的数目。
第一类stirling数递推公式:
S(n,0)=0
S(1,1)=1
S(n,k)=S(n-1,k-1)+(n-1)S(n-1,k)
对于
第一类stirling数递推关系的理解:
第n个元素单独一个环时其他元素的情况:
S(n-1
,k-1);
第n个元素和其他元素构成k个环时,它和第i个元素是挨着的(放在左边),有(n-1)S(n-1,k)种情况。所以结果就是S(n-1,k-1)+(n-1)S(n-1,k)
第二类stirling数递推公式:
S(n,k)=0(k>n or k=0)
S(n,1)=S(n,n)=1
S(n,k)=S(n-1,k-1)+kS(n-1,k)
对于第二类stirling数递推关系的理解:
第n个元素单独占一个子集时其他元素的情况:
S(n-1,k-1);第n个元素和其他元素呆在同一个子集时有kS(n-1,k)种情况。所以结果就是S(n-1,k-1)+kS(n-1,k)
相关题目:
POJ 1430 Binary Stirling Numbers
http://poj.org/problem?id=1430
大意:第二类stirling数,递推关系给出了,但是数据量巨大,求解结果mod 2.
下面仅仅是自己的一点理解,看了别人的博文半天都没懂。。。
分析:由递推关系dp[n,k]=dp[n-1,k-1]+kdp[n-1,k]
当k时偶数时,dp[n,k]=dp[n-1][k-1]
当k是奇数时,dp[n,k]=
dp[n-1,k-1]+kdp[n-1,k]=dp[n-2,k-2]+kdp[n-1,k]
这种递推的场景很像Pascal,同样的,把Pascal的数形结合的思想用于此题。
但是好像有点不同,是的。
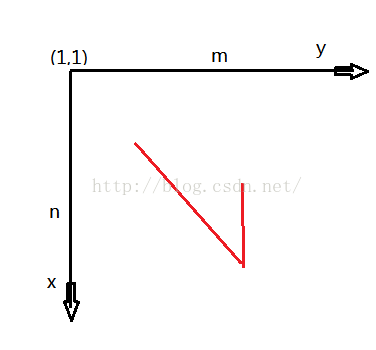
对于斜方向的向量,它在Y轴的分量是这样的:
8->
7->5->3->1
9->
7->5->3->1
它走奇数的路线,所以在y轴(X轴)方向的步数(分量)应该是m/2. 由(1,1)->(n,m)X轴方向一共有n-1步,所以竖着走贡献的步数就该是n-1-m/2。单纯的Y轴方向走时,有(m-1)/2步数 【仅仅走奇数】
答案就是 ans=C(n-1-m/2,(m-1)/2)=C(A,B)=A!/(B! (A-B)!)
接下来。。。
素因子的思想又闪亮登场了!
统计分子分母的2的个数相比较即可。
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
LL get(LL x){
if(x==0) return 0LL;
return x/2+get(x/2);
}
int main()
{
LL d,n,m;
cin>>d;
while(d--){
scanf("%lld%lld",&n,&m);
LL A=n-1-m/2;
LL B=(m-1)/2;
LL q1=get(A),q2=get(B),q3=get(A-B);
if(q1-q2-q3>0) puts("0");
else puts("1");
}
return 0;
}
hdu 3625
Examining the Rooms
http://acm.hdu.edu.cn/showproblem.php?pid=3625
分析:如果能打开这些房间,那么所有的房间一定是成环的(或者说钥匙是成环的),环的个数有可能是1个,2个,……,k个。这是第一类stirling数。但是要求不能炸毁一号房间,如果一号房间的钥匙就在一号房间那么我们永远也打不开一号房间,所以一号房间不能单独成环。即对于m个环,总的方案数应该是s(n,m)-s(n-1,m-1)。
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
LL s[25][25],fac[25];
int main()
{
//freopen("cin.txt","r",stdin);
s[1][1]=1;
for(int i=2;i<=20;i++){
for(int j=1;j<=i;j++){
s[i][j]=s[i-1][j-1]+(i-1)*s[i-1][j];
}
}
fac[1]=1;
for(int i=2;i<25;i++) fac[i]=fac[i-1]*i;
int t,n,k;
cin>>t;
while(t--){
scanf("%d%d",&n,&k);
LL sum=0;
for(int i=1;i<=k;i++){
sum=sum+s[n][i]-s[n-1][i-1]; //除去1号房间单独成环的情况
}
printf("%.4lf\n",1.0*sum/fac[n]);
}
return 0;
}