UVALive 7461 - Separating Pebbles
传送门
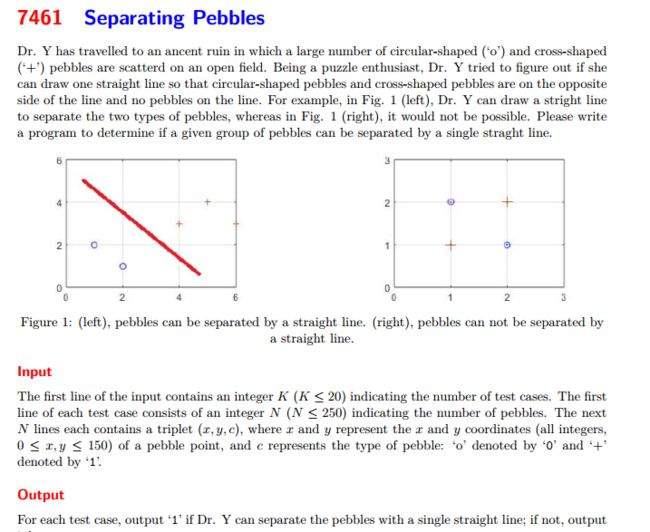
题目大意:
给一个数N,然后每行3个数,前两个数十坐标,后面的一个数区分是 ‘+’ 还是’o’,0代表的是’o’,1代表的是’+’.然后判断是不是能够有一条线把这两部分分开也就是线的两边都是一样的标识符。如果能输出1, 否则输出 0.
解题思路:
其实,我们可以将’o’代表的所有的点构成一个凸包,将’+’代表的所有的点构成一个凸包,判断这两个凸包是不是有相交就行了。
My Code:
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <queue>
using namespace std;
///基础点和向量运算
struct Point
{
double x,y;
Point(double x=0,double y=0):x(x),y(y) {}
};
typedef Point Vector;
Vector operator + (Vector A,Vector B)
{
return Vector(A.x+B.x,A.y+B.y);
}
Vector operator - (Vector A,Vector B)
{
return Vector(A.x-B.x,A.y-B.y);
}
Vector operator * (Vector A,double p)
{
return Vector(A.x*p,A.y*p);
}
Vector operator / (Vector A,double p)
{
return Vector(A.x/p,A.y/p);
}
bool operator <(const Point& a, const Point& b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
const double eps=1e-10;
int dcmp(double x)///判断正负,或者等于0
{
if(fabs(x)<eps)return 0;
else return x<0?-1:1;
}
bool operator==(const Point& a,const Point &b)
{
return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double Dot(Vector A, Vector B)
{
return A.x*B.x+A.y*B.y; ///点积
}
double Length(Vector A)
{
return sqrt(Dot(A,A)); ///OA长
}
double Angle(Vector A,Vector B)
{
return acos(Dot(A,B)/Length(A)/Length(B)); ///OA和OB的夹角
}
double Cross(Vector A,Vector B)
{
return A.x*B.y-A.y*B.x; ///叉积
}
double Area2(Point A,Point B,Point C)
{
return Cross(B-A,C-A); ///三角形面积
}
Vector Rotate(Vector A,double rad)///rad为弧度,旋转rad度
{
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
Vector Normal(Vector A)///A的单位法向量,A不能为零向量
{
double L=Length(A);
return Vector(-A.y/L,A.x/L);
}
///点和直线
///P+tv表示一条直线,P为点,tv为方向向量
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)///求直线交点,确保存在交点,即Cross(v,w)非0
{
Vector u=P-Q;
double t=Cross(w,u)/Cross(v,w);
return P+v*t;
}
double DistanceToLine(Point P,Point A,Point B)///P点到直线AB的距离
{
Vector v1=B-A,v2=P-A;
return fabs(Cross(v1,v2)/Length(v1));
}
double DistanceToSegment(Point P,Point A,Point B)///点P到线段AB的距离
{
if(A==B)return Length(P-A);
Vector v1=B-A,v2=P-A,v3=P-B;
if(dcmp(Dot(v1,v2))<0)return Length(v2);
else if(dcmp(Dot(v1,v3))>0)return Length(v3);
else return fabs(Cross(v1,v2)/Length(v1));
}
Point GetLineProjection(Point P,Point A,Point B)///点在直线上的投影
{
Vector v=B-A;
return A+v*(Dot(v,P-A)/Dot(v,v));
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)///判断线段相交,不在端点相交
{
double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
bool OnSegment(Point p,Point a1,Point a2)///判断点是否在线段上(不包括端点)
{
return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p))<0;
}
///多边型
double ConvexPolygonArea(Point* p,int n)///多边形面积,,点按顺序
{
double area=0;
for(int i=1; i<n-1; i++)
area+=Cross(p[i]-p[0],p[i+1]-p[0]);
return area/2;
}
const int maxn=1e3+10;
int ConvexHull(Point *p,Point *ch,int n)///求凸包
{
sort(p,p+n);
int i,m=0,k;
for(i=0; i<n; i++)
{
while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
ch[m++]=p[i];
}
k=m;
for(i=n-2; i>=0; i--)
{
while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;
ch[m++]=p[i];
}
if(n>1)m--;
return m;
}
///if(ConvexHullIntersection(ch1,t1,ch2,t2)&&ConvexHullIntersection(ch2,t2,ch1,t1))printf("YES\n");else printf("NO\n");
bool ConvexHullIntersection(Point *ch1,int t1,Point *ch2,int t2)///判断凸包是否相交
{
double angle[maxn],x;
int i,j,k,m;
if(t1==1)return true;
if(t1==2)
{
for(i=0; i<t2; i++)
{
k=dcmp(Cross(ch1[1]-ch1[0],ch2[i]-ch1[0]));
if(k==0&&Dot(ch1[1]-ch1[0],ch2[i]-ch1[0])>0)
{
if(Length(ch2[i]-ch1[0])<Length(ch1[1]-ch1[0]))break;
}
}
if(i<t2)return false;
if(t2==2&&SegmentProperIntersection(ch1[0],ch1[1],ch2[0],ch2[1]))return false;
return true;
}
angle[0]=0;
for(i=2; i<t1; i++)
angle[i-1]=Angle(ch1[1]-ch1[0],ch1[i]-ch1[0]);
for(i=0; i<t2; i++)
{
j=dcmp(Cross(ch1[1]-ch1[0],ch2[i]-ch1[0]));
if(j<0||(j==0&&Dot(ch1[1]-ch1[0],ch2[i]-ch1[0])<0))continue;
j=dcmp(Cross(ch1[t1-1]-ch1[0],ch2[i]-ch1[0]));
if(j>0||(j==0&&Dot(ch1[t1-1]-ch1[0],ch2[i]-ch1[0])<0))continue;
x=Angle(ch1[1]-ch1[0],ch2[i]-ch1[0]);
m=lower_bound(angle,angle+t1-1,x)-angle;
if(m==0)j=0;
else j=m-1;
k=dcmp(Cross(ch1[j+1]-ch2[i],ch1[j+2]-ch2[i]));
if(k>=0)break;
}
if(i<t2)return false;
return true;
}
Point p1[maxn],ch1[maxn],p2[maxn],ch2[maxn], p[maxn];
int n,m,t1,t2;
int main()
{
int T;
cin>>T;
while(T--)
{
int sum;
cin>>sum;
int i,j,k, n = 0, m = 0, op;
for(i=0; i<sum; i++)
{
scanf("%lf%lf%d",&p[i].x,&p[i].y,&op);
if(op==0)
{
p1[n].x = p[i].x;
p1[n++].y = p[i].y;
}
else
{
p2[m].x = p[i].x;
p2[m++].y = p[i].y;
}
}
t1=ConvexHull(p1,ch1,n);
t2=ConvexHull(p2,ch2,m);
if(ConvexHullIntersection(ch1,t1,ch2,t2)&&ConvexHullIntersection(ch2,t2,ch1,t1))
puts("1");
else
puts("0");
}
return 0;
}