codeforces:405C - Unusual Product 规律异或
Little Chris is a huge fan of linear algebra. This time he has been given a homework about the unusual square of a square matrix.
The dot product of two integer number vectors x and y of size n is the sum of the products of the corresponding components of the vectors. The unusual square of an n × n square matrix A is defined as the sum of n dot products. The i-th of them is the dot product of the i-th row vector and the i-th column vector in the matrix A.
Fortunately for Chris, he has to work only in GF(2)! This means that all operations (addition, multiplication) are calculated modulo 2. In fact, the matrix A is binary: each element of A is either 0 or 1. For example, consider the following matrix A:
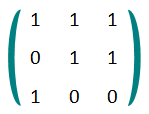
The unusual square of A is equal to (1·1 + 1·0 + 1·1) + (0·1 + 1·1 + 1·0) + (1·1 + 0·1 + 0·0) = 0 + 1 + 1 = 0.
However, there is much more to the homework. Chris has to process q queries; each query can be one of the following:
- given a row index i, flip all the values in the i-th row in A;
- given a column index i, flip all the values in the i-th column in A;
- find the unusual square of A.
To flip a bit value w means to change it to 1 - w, i.e., 1 changes to 0 and 0 changes to 1.
Given the initial matrix A, output the answers for each query of the third type! Can you solve Chris's homework?
The first line of input contains an integer n (1 ≤ n ≤ 1000), the number of rows and the number of columns in the matrix A. The next nlines describe the matrix: the i-th line contains n space-separated bits and describes the i-th row of A. The j-th number of the i-th lineaij (0 ≤ aij ≤ 1) is the element on the intersection of the i-th row and the j-th column of A.
The next line of input contains an integer q (1 ≤ q ≤ 106), the number of queries. Each of the next q lines describes a single query, which can be one of the following:
- 1 i — flip the values of the i-th row;
- 2 i — flip the values of the i-th column;
- 3 — output the unusual square of A.
Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.
Let the number of the 3rd type queries in the input be m. Output a single string s of length m, where the i-th symbol of s is the value of the unusual square of A for the i-th query of the 3rd type as it appears in the input.
3 1 1 1 0 1 1 1 0 0 12 3 2 3 3 2 2 2 2 1 3 3 3 1 2 2 1 1 1 3
01001
这题有点神……刚开始用了暴力不机智T了一发,然后一直在想怎么改进,晕……果断看到别人的几行就搞定了……唉……顿觉自己弱了好多,一直觉得C题应该代码都得多点嘛,没想到又被坑了……不机智啊!!!
思路:因为是第一行乘以第一列,第二行乘以第二列……所以只有a[i][i] 乘了自己一次,其他都是互相乘了两次,既然乘了两次,那么只有两种情况,一种是0*1=0+0=0,另 一种是(1*1+1*1)%2=0,这两种模2后都等于0,所以这些都不需要算了……既然是模2,那么直接用异或来算都可以了……当把每行或者每列的每个值都由0变1或者由1变0后,那么主对角线的肯定有一个值变了,所以结果值再异或1就行了嘛!!!
不过这题是比较特殊的,因为是模2了,所以可以用异或来算,并且矩阵的值都是0或者1,有点特殊,如果不是模2并且值可以是任意的话,那该怎么快速做出来呢,即在1s内得出答案呢???这个我还没想好……自己的暴力T了,现在还在想当中……
#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <list>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#define PI acos(-1.0)
#define mem(a,b) memset(a,b,sizeof(a))
#define sca(a) scanf("%d",&a)
#define pri(a) printf("%d\n",a)
#define lson i<<1,l,mid
#define rson i<<1|1,mid+1,r
#define MM 1005
#define Max 2
#define INF 55566677
#define eps 1e-7
using namespace std;
typedef long long ll;
char s[1000010];
int main()
{
int n,i,j,k,q,ans=0,cnt=0;
sca(n);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
sca(k);
if(i==j) ans^=k;
}
sca(q);
while(q--)
{
sca(k);
if(k==3) s[cnt++]=ans+'0';
else sca(k),ans^=1;
}
s[cnt]=0;
puts(s);
return 0;
}