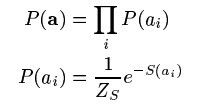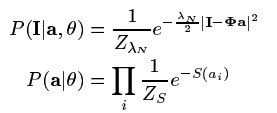稀疏编码(Sparse Coding)(二)
为了更进一步的清晰理解大脑皮层对信号编码的工作机制(策略),需要把他们转成数学语言,因为数学语言作为一种严谨的语言,可以利用它推导出期望和要寻找的程式。本节就使用概率推理(bayes views)的方式把稀疏编码扩展到随时间变化的图像上,因为人类或者哺乳动物在日常活动中通过眼睛获取的信号是随时间变化而变化的,对于此类信号仍然有一些稀疏系数和基可以描述他们,同类型的处理方式也有慢特征分析(slow features analysis)。废话不多说了,进入正题:
我们把图像流(图像序列)![]() 看成时空基函数
看成时空基函数![]() 的线性组合再加上一些噪声
的线性组合再加上一些噪声![]() ,当然时空基函数可以想象成是时空不变的,类似于行为识别里的3D-SIFT,这点貌似又和慢特征分析扯上关系咯。同样时空基函数仍然有一些系数
,当然时空基函数可以想象成是时空不变的,类似于行为识别里的3D-SIFT,这点貌似又和慢特征分析扯上关系咯。同样时空基函数仍然有一些系数![]() ,用表示,则图像流则可以看成时空基和系数的卷积加上一些噪声,其模型如(公式一)所示:
,用表示,则图像流则可以看成时空基和系数的卷积加上一些噪声,其模型如(公式一)所示:
(公式一)
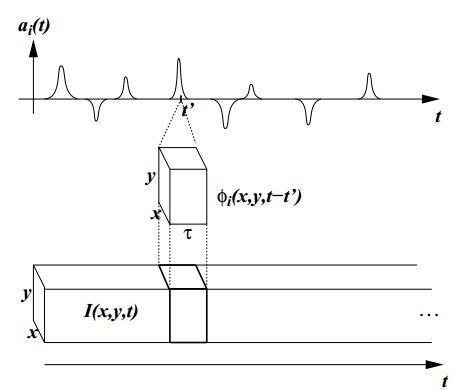
整个模型可以形象的用(图一)展示,注意系数是一种单峰类似刺突的东东哦,(图一)上:
(图一)
当然对于(图一)中的时空基函数![]() 应尽可能的稀疏,便于减少运算量,不然对图像序列的运算量太大了。对于模型的参数求解,先假设系数独立且满足稀疏,bruno基于这些假设,给出了系数的先验公式,如(公式二)所示:
应尽可能的稀疏,便于减少运算量,不然对图像序列的运算量太大了。对于模型的参数求解,先假设系数独立且满足稀疏,bruno基于这些假设,给出了系数的先验公式,如(公式二)所示:
(公式二)
因为系数之间独立,所以他们的联合分布分解成单个分布的乘积形式,而且每个系数满足稀疏假设,S是个非凸函数控制着系数alpha的稀疏。有了这些先验知识,给定图像序列后的系数alpha的后验概率如(公式三)所示:
(公式三)
通过最大化此后验概率,然后利用其梯度下降法求解,求的系数alpha,全部求解步骤如(公式四)所示:
(公式四)
公式尽管这么多,但扔不足以说明求解系数的详细步骤,因为(公式三)的后两项仍然不清楚,再次对这二项再做个假设,如(公式五)所示:
(公式五)
尽管做了如此假设,但是P(I|alpha,theta)仍然不能直接计算,需要对此项采样方能完成,这个地方是需要改进的地方,尽管如此,我们还是硬着头皮把学习基函数步骤一并贴出来,为后续改进打下铺垫。学习过程如(图二)所示:
(图二)
系数alpha通过梯度下降完成,基函数更新则通过Hebbian learning学习完成,Hebbian(海扁,又译赫布)学习就是加强同时激活的细胞之间的连接("Cells that firetogether, wire together."),这点可以稍微解释了“读书百遍”背后的大脑皮层可塑的工作机制。学习到的基函数如(图三)所示:
(图三)
好咯,稀疏编码的生命科学的解释到此就差不多了,可以看到思想不错,但是手工假设的太多,学习方法也不友好,随着代数学以及LASSO的引入,稀疏码逐渐开始成熟,并开始走上应用的道路,到了DeepLearning时代,手工成分也越来越少,威力貌似也越来越大。(好吧,我承认这节写的很恶心![]() ,但是这节最大的亮点就是在空时域上编码,这对行为识别、语言识别啥的都有些帮助哦)
,但是这节最大的亮点就是在空时域上编码,这对行为识别、语言识别啥的都有些帮助哦)
参考文献:
Probabilistic Models of the Brain: Perception and Neural Function. MIT Press
转载请注明链接:http://blog.csdn.net/cuoqu/article/details/8989233