偏见方差的权衡(Bias Variance Tradeoff)
RSS看起来是一个非常合理的统计模型优化目标。但是考虑k-NN的例子,在最近邻的情况下(k=1),RSS=0,是不是k-NN就是一个完美的模型了呢,显然不是k-NN有很多明显的问题,比如对训练数据量的要求很大,很容易陷入维度灾难中。
k-NN的例子说明仅仅优化RSS是不充分的,因为针对特定训练集合拟合很好的model,并不能说明这个model的泛化能力好,而泛化能力恰恰又是机器学习模型的最重要的要求。真正能说明问题的不是RSS,因为它只是一个特定训练集合,而是在多个训练结合统计得出的RSS的期望,MSE(mean squared error),而MSE又可以拆分成bias和variance两部分: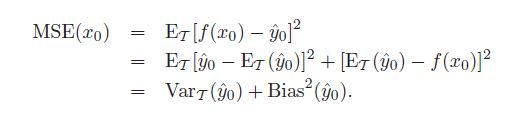
式子的推导很显然,只要填一项减一项,展开式子,多余的那一项等于0
从上面的式子可以看出,低bias的model在训练集合上更加准确,低variance的model在不同的训练集合上性能更加稳定。
Bias 度量了某种学习算法的平均估计结果所能逼近学习目标的程度;独立于训练样本的误差,刻画了匹配的准确性和质量:一个高的bias意味着一个坏的匹。
Variance 则度量了在面对同样规模的不同训练集时,学习算法的估计结果发生变动的程度。相关于观测样本的误差,刻画了一个学习算法的精确性和特定性:一个高的variance意味着一个弱的匹配。
举两个极端的例子:
- 记住训练集合上所有的点的label,这样的系统低bias,高variance
- 无论输入是什么,总是预测一个相同的,这样的系统高bias,低variance。
因此在一个model的选择上需要进行偏倚和方差的权衡。
显然复杂的模型能更好的拟合训练集合能更好的拟合训练集合上的点,但是同时高复杂度的模型泛化能力差,造成了高方差。横坐标的右侧是overfitting的情况,而左侧是underfitting的情况。
可见如果目标函数只是优化RSS那么在有限训练集合的情况下,很难训练出一个效果好的模型,想一下在分类中表现比较好的SVM基于maxiumu margin的思想,而maxent考虑的是熵的最大,均是增加泛化能力,降低模型复杂度的手段。
一个较好的选择是改进优化函数,在优化RSS的同时,惩罚复杂模型
参考链接:
http://goo.gl/mZwum
